题目内容
已知ABCD是矩形,边长AB=3,BC=4,正方形ACEF边长为5,平面ACEF⊥平面ABCD,则多面体ABCDEF的外接球的表面积 ( )
A.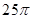 | B.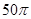 | C.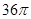 | D.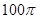 |
B
解析试题分析:解:由题意作出图形: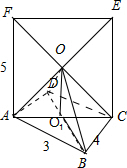
分别连接矩形ABCD和正方形ACEF的对角线,分别相较于点O1、O,由球的截面圆的性质可知:球心必在过O1与平面ABCD垂直的直线上和在过点O且平面ACEF垂直的直线上,因此球心必为二直线 的交点即点O.(也可以证明得O到所有顶点的距离都相等).∴球的半径为R= =
=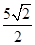 ,∴多面体ABCDEF的外接球的表面积S=4π×(
,∴多面体ABCDEF的外接球的表面积S=4π×(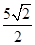 )2=50π.故答案为B
)2=50π.故答案为B
考点:球的截面圆
点评:熟练掌握球的截面圆的性质是解题的关键

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案设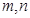 是两条不同的直线,
是两条不同的直线,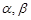 是两个不同的平面,有下列四个命题:
是两个不同的平面,有下列四个命题:
① 若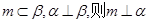 ; ② 若
; ② 若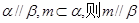 ;
;
③ 若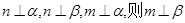 ; ④ 若
; ④ 若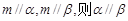
其中正确命题的序号是( )
| A.①③ | B.①② | C.③④ | D.②③ |
如图,二面角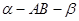 与
与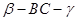 均为
均为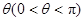 ,
,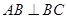 ,
,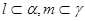 ,则下列不可能成立的是( )
,则下列不可能成立的是( )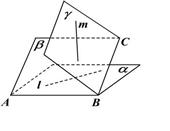
A.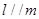 | B.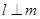 |
C.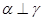 | D.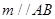 |
在空间中,下列命题正确的是
| A.平行于同一平面的两条直线平行 | B.垂直于同一平面的两条直线平行 |
| C.平行于同一直线的两个平面平行 | D.垂直于同一平面的两个平面平行 |
下列命题中正确的个数是( )
①若直线a不在α内,则a∥α;
②若直线l上有无数个点不在平面α内,则l∥α;
③若直线l与平面α平行,则l与α内的任意一条直线都平行;
④若l与平面α平行,则l与α内任何一条直线都没有公共点;
⑤平行于同一平面的两直线可以相交.
| A.1 | B.2 | C.3 | D.4 |
用M表示平面, 表示一条直线,则M内至少有一直线与
表示一条直线,则M内至少有一直线与 ( )
( )
| A.平行; | B.相交; | C.异面; | D.垂直。 |
设m,n是两条不同直线,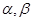 是两个不同的平面,给出下列四个命题
是两个不同的平面,给出下列四个命题
①若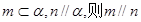 ②
②
③若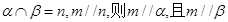 ④若
④若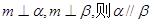
其中正确的命题是 ( )
| A.① | B.② | C.③④ | D.②④ |
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8 | B.16 : : | C.14 | D.18 |
已知正四棱锥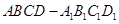 中,
中,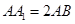 ,则CD与平面
,则CD与平面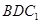 所成角的正弦值等于( )
所成角的正弦值等于( )
A.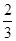 | B.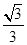 | C.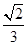 | D.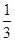 |