题目内容
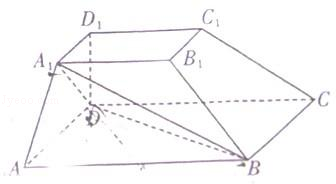
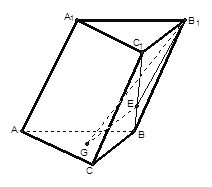
(2011•山东)如图,在四棱台ABCD﹣A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.

(1)见解析 (2)见解析
(1)∵D1D⊥平面ABCD,
∴D1D⊥BD.
又AB=2AD,AD=A1B1,∠BAD=60°,
△ABD 中,由余弦定理得
BD2=AD2+AB2﹣2AB•ADcos60°=3AD2,
∴AD2+BD2=AB2,
∴AD⊥BD,又 AD∩DD1=D,∴BD⊥面ADD1A1.
由 AA1?面ADD1A1,
∴BD⊥AA1.
(2)证明:连接AC 和A1C1,设 AC∩BD=E,由于底面ABCD是平行四边形,故E为平行四边形ABCD的
中心,由棱台的定义及AB=2AD=2A1B1,可得 EC∥A1C1,且 EC=A1C1,
故ECC1 A1为平行四边形,∴CC1∥A1 E,而A1 E?平面A1BD,∴CC1∥平面A1BD.
∴D1D⊥BD.
又AB=2AD,AD=A1B1,∠BAD=60°,
△ABD 中,由余弦定理得
BD2=AD2+AB2﹣2AB•ADcos60°=3AD2,
∴AD2+BD2=AB2,
∴AD⊥BD,又 AD∩DD1=D,∴BD⊥面ADD1A1.
由 AA1?面ADD1A1,
∴BD⊥AA1.
(2)证明:连接AC 和A1C1,设 AC∩BD=E,由于底面ABCD是平行四边形,故E为平行四边形ABCD的
中心,由棱台的定义及AB=2AD=2A1B1,可得 EC∥A1C1,且 EC=A1C1,
故ECC1 A1为平行四边形,∴CC1∥A1 E,而A1 E?平面A1BD,∴CC1∥平面A1BD.

练习册系列答案
相关题目
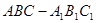 中,侧面
中,侧面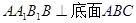 ,
,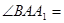
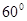 ,
,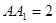 ,底面
,底面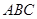 是边长为
是边长为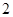 的正三角形,其重心为
的正三角形,其重心为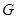 点,
点,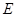 是线段
是线段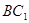 上一点,且
上一点,且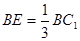 .
.
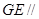 侧面
侧面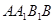 ;
;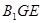 与底面
与底面 中,
中,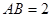 ,
, 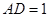 ,
,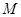 为
为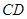 的中点.将
的中点.将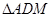 沿
沿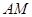 折起,使得平面
折起,使得平面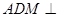 平面
平面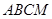 .
.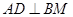 ;
; 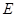 是线段
是线段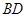 的中点,求二面角
的中点,求二面角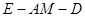 的余弦值.
的余弦值.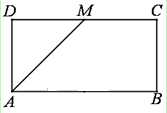
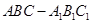 的侧棱与底面垂直,且
的侧棱与底面垂直,且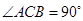 ,
,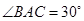 ,
,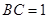 ,
,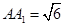 ,点
,点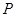 、
、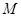 、
、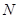 分别为
分别为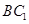 、
、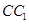 、
、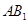 的中点.
的中点.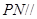 平面
平面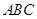 ;
;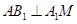 ;
;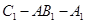 的余弦值.
的余弦值.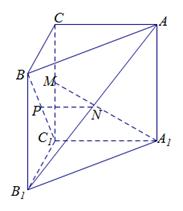
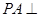 平面ABCD,AD//BC,
平面ABCD,AD//BC,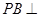 AC,
AC,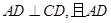
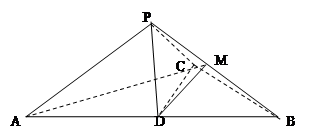
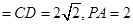 ,点M在线段PD上.
,点M在线段PD上.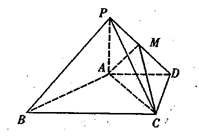
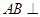 平面PAC;
平面PAC; ,试确定点M的位置.
,试确定点M的位置.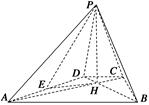
 .
.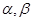 是两个不同的平面,
是两个不同的平面,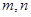 是平面
是平面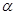 及
及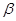 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断: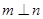 ②
②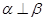 ③
③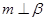 ④
④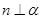 。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.