题目内容
设m,n是两条不同直线,α,β是两个不同的平面,下列命题正确的是( )
| A.m∥α,n∥β且α∥β,则m∥n |
| B.m⊥α,n⊥β且α⊥β,则m⊥n |
| C.m⊥α,n?β,m⊥n,则α⊥β |
| D.m?α,n?α,m∥β,n∥β,则α∥β |
B
对于A,若m∥α,n∥β且α∥β,说明m、n是分别在平行平面内的直线,它们的位置关系应该是平行或异面,故A错;
对于B,由m⊥α,n⊥β且α⊥β,则m与n一定不平行,否则有α∥β,与已知α⊥β矛盾,通过平移使得m与n相交,
且设m与n确定的平面为γ,则γ与α和β的交线所成的角即为α与β所成的角,因为α⊥β,所以m与n所成的角为90°,
故命题B正确.
对于C,根据面面垂直的性质,可知m⊥α,n?β,m⊥n,∴n∥α,∴α∥β也可能α∩β=l,也可能α⊥β,故C不正确;
对于D,若“m?α,n?α,m∥β,n∥β”,则“α∥β”也可能α∩β=l,所以D不成立.
故选B.
对于B,由m⊥α,n⊥β且α⊥β,则m与n一定不平行,否则有α∥β,与已知α⊥β矛盾,通过平移使得m与n相交,
且设m与n确定的平面为γ,则γ与α和β的交线所成的角即为α与β所成的角,因为α⊥β,所以m与n所成的角为90°,
故命题B正确.
对于C,根据面面垂直的性质,可知m⊥α,n?β,m⊥n,∴n∥α,∴α∥β也可能α∩β=l,也可能α⊥β,故C不正确;
对于D,若“m?α,n?α,m∥β,n∥β”,则“α∥β”也可能α∩β=l,所以D不成立.
故选B.

练习册系列答案
相关题目
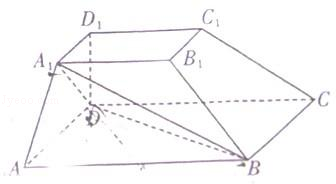

 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点.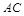 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 ⊥A1C.
⊥A1C.

 平面
平面 .
. 平面
平面 平面
平面 ,直线
,直线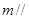 平面
平面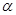 ,则
,则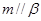 ;
;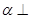 平面
平面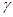 ,且平面
,且平面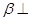 平面
平面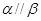 ;
;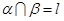 ,点
,点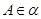 ,
,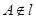 ,若直线
,若直线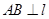 ,则
,则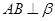 ;
;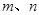 为异面直线,且
为异面直线,且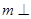 平面
平面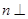 平面
平面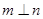 ,则
,则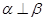 .
. 
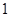
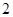
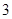
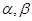 表示平面,m,n表示直线,
表示平面,m,n表示直线, 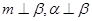 ,给出下列四个结论:
,给出下列四个结论: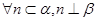 ;②
;②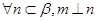 ;③
;③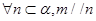 ;④
;④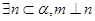 ,
,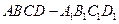 的棱长为a,M、N分别为
的棱长为a,M、N分别为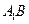 和AC上的点,
和AC上的点,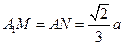 ,则MN与平面
,则MN与平面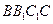 的位置关系是( )
的位置关系是( )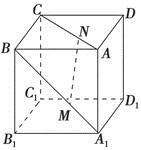
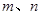 是两条不同的直线,
是两条不同的直线,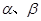 是两个不同的平面。下列四个命题正确的是( )
是两个不同的平面。下列四个命题正确的是( )


