题目内容
已知函数f(x)＝x2－2ax＋5在(－∞，2]上是减函数，且对任意的x1，x2∈[1，a＋1]，总有|f(x1)－f(x2)|≤4，则实数a的取值范围为______．
[2,3]
函数f(x)＝(x－a)2＋5－a2在(－∞，2]上是减函数，∴a≥2，函数f(x)在[1，a]上是减函数，在[a，a＋1]上是增函数，要使x1，x2∈[1，a＋1]时，总有|f(x1)－f(x2)|≤4，
只要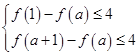
又f(1)≥f(a＋1)，∴只要f(1)－f(a)≤4，即(6－2a)－(5－a2)≤4，解得－1≤a≤3.又a≥2，故2≤a≤3.
只要
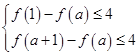
又f(1)≥f(a＋1)，∴只要f(1)－f(a)≤4，即(6－2a)－(5－a2)≤4，解得－1≤a≤3.又a≥2，故2≤a≤3.
练习册系列答案
相关题目
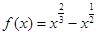，则满足
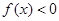的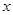
取值范围是 .
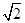)，试确定m的值，并求满足条件f(2－a)>f(a－1)的实数a的取值范围．
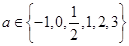，则使函数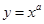
的定义域为R且为奇函数的所有
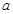的值有（ ）
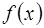存在反函数，且反函数
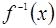过点（2，4），则
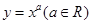图像经过不等式组
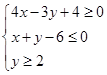表示的区域，则a的取值范围是
