Question

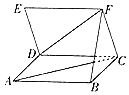
【题目】已知两个正方形ABCD和CDEF有一条公共边CD，且△BCF是等边三角形，则异面直线AC和DF所成角的余弦值为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

取CD的中点M，CF的中点N，连接MN，可得MN//DF．延长BC到P，使CPBC，连接MP，NP．异面直线AC和DF所成角为∠NMP，△NMP中，利用余弦定理即可得出．

取CD的中点M，CF的中点N，连接MN，延长BC到P，使CPBC，连接MP，NP，如图，

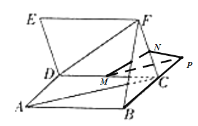
则MN//DF,由可得 MP//AC．

令AB＝2，则MP=MN，

又△BCF是等边三角形，NC=PC=1，

由余弦定理可得：，

异面直线AC和DF所成角为∠NMP（或其补角），

∴cos∠NMP．

异面直线AC和DF所成角的余弦值为.

故选：B．