题目内容
已知椭圆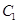 :
: 的离心率为
的离心率为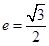 且与双曲线
且与双曲线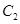 :
: 有共同焦点.
有共同焦点.
(1)求椭圆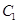 的方程;
的方程;
(2)在椭圆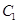 落在第一象限的图像上任取一点作
落在第一象限的图像上任取一点作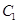 的切线
的切线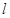 ,求
,求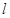 与坐标轴围成的三角形的面积的最小值;
与坐标轴围成的三角形的面积的最小值;
(3)设椭圆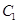 的左、右顶点分别为
的左、右顶点分别为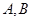 ,过椭圆
,过椭圆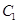 上的一点
上的一点 作
作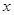 轴的垂线交
轴的垂线交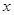 轴于点
轴于点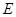 ,若
,若 点满足
点满足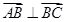 ,
,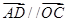 ,连结
,连结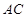 交
交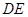 于点
于点 ,求证:
,求证: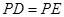 .
.
(1)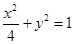 ;(2)2;(3)证明详见解析.
;(2)2;(3)证明详见解析.
解析试题分析:(1)有离心率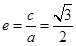 ,求得
,求得 (s),由公共焦点得
(s),由公共焦点得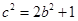 即
即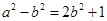 (t),解由(s)(t)组成的方程组即可.
(t),解由(s)(t)组成的方程组即可.
(2)设直线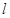 的方程为:
的方程为: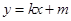
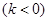 ,代入椭圆
,代入椭圆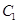 方程中,消去y,得到关于x的一元二次方程,其判别式等于零,可得
方程中,消去y,得到关于x的一元二次方程,其判别式等于零,可得 ,在求出直线l与坐标轴的交点,写出围成的三角形的面积
,在求出直线l与坐标轴的交点,写出围成的三角形的面积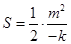 ,再把
,再把 代入,即可最的最小值.
代入,即可最的最小值.
(3)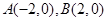 ,设
,设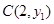 ,
, ,求出
,求出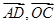 的坐标,由向量平行的充要条件可得
的坐标,由向量平行的充要条件可得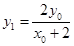 ,在求出直线AC的方程,整理得
,在求出直线AC的方程,整理得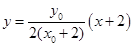 ,然后求出P点坐标即可.
,然后求出P点坐标即可.
试题解析:(1)由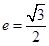 可得:
可得: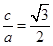 即
即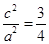
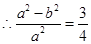
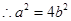 ① 2分
① 2分
又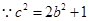 即
即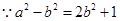 ②联立①②解得:
②联立①②解得: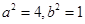
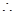 椭圆
椭圆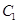 的方程为:
的方程为: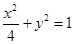 3分
3分
(2)
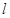 与椭圆
与椭圆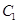 相切于第一象限内的一点,
相切于第一象限内的一点,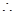 直线
直线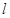 的斜率必存在且为负
的斜率必存在且为负
设直线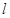 的方程为:
的方程为: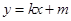
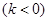
联立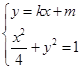 消去
消去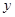 整理可得:
整理可得: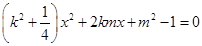 ③, 4分
③, 4分
根据题意可得方程③只有一实根,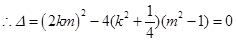 整理可得:
整理可得: ④ 6分
④ 6分 直线
直线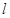 与两坐标轴的交点分别为
与两坐标轴的交点分别为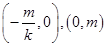 且
且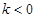 7分
7分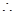
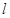 与坐标轴围成的三角形的面积
与坐标轴围成的三角形的面积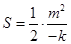 ⑤, 8分
⑤, 8分
④代入⑤可得: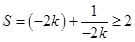 (当且仅当
(当且仅当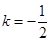 时取等号) 9分
时取等号) 9分
(3)由(1)得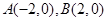 ,设
,设 ,
,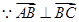 ,
,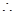 可设
可设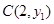 ,
,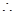
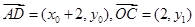
由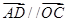 可得:
可得: 即
即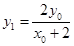 11分
11分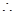 直线
直线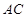 的方程为:
的方程为: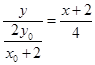 整理得:
整理得: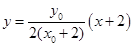
点 在
在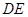 上,令
上,令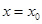 代入直线
代入直线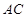 的方程可得:
的方程可得: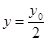 , 13分
, 13分
即点 的坐标为
的坐标为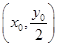
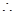
 为
为
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
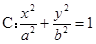
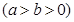 过点
过点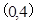 ,离心率为
,离心率为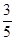 .
.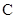 的方程;
的方程;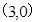 且斜率为
且斜率为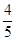 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标.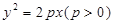 ,其准线方程为
,其准线方程为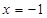 ,过准线与
,过准线与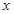 轴的交点
轴的交点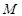 做直线
做直线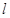 交抛物线于
交抛物线于 两点.
两点.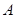 为
为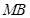 中点,求直线
中点,求直线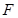 ,当
,当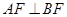 时,求
时,求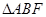 的面积.
的面积.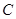 :
: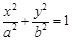 (
(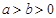 )过点
)过点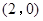 ,且椭圆
,且椭圆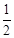 .
.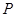 在直线
在直线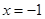 上,过
上,过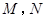 两点,且
两点,且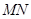 中点,再过
中点,再过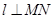 .证明:直线
.证明:直线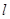 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.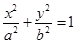
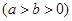 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为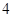 ,且过点
,且过点 .
. 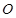 为坐标原点,斜率为
为坐标原点,斜率为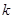 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点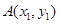 ,
,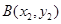 ,若
,若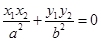 ,求△
,求△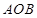 的面积.
的面积. ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为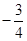 .
.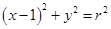 (
(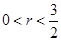 )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.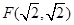 及直线
及直线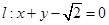 ,曲线
,曲线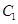 是满足下列两个条件的动点
是满足下列两个条件的动点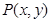 的轨迹:①
的轨迹:①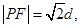 其中
其中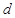 是
是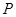 到直线
到直线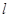 的距离;②
的距离;②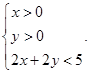
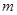 与曲线
与曲线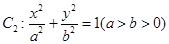 均相切于同一点,求椭圆
均相切于同一点,求椭圆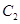 离心率
离心率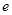 的取值范围.
的取值范围.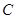 的一个焦点为
的一个焦点为 ,过点
,过点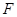 且垂直于长轴的直线被椭圆
且垂直于长轴的直线被椭圆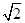 ;
;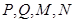 为椭圆
为椭圆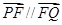 ,
,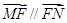 且
且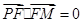 ,求四边形
,求四边形 的面积的最大值和最小值.
的面积的最大值和最小值.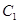 的方程为
的方程为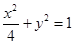 ,双曲线
,双曲线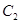 的左、右焦点分别为
的左、右焦点分别为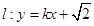 与椭圆
与椭圆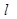 与
与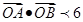 (其中0为原点),求k的取值范围。
(其中0为原点),求k的取值范围。