题目内容
已知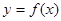 (
( ,
, 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数 在
在 内单调递增或单调递减;②如果存在区间
内单调递增或单调递减;②如果存在区间 ,使函数
,使函数 在区间
在区间 上的值域为
上的值域为 ,那么称
,那么称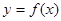 ,
, 为闭函数
为闭函数
(1)判断函数 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(2)求证:函数 (
( )为闭函数;
)为闭函数;
(3)若 是闭函数,求实数
是闭函数,求实数 的取值范围
的取值范围
【答案】
解:(1)函数 在区间
在区间 上单调递减,在
上单调递减,在 上单调递增;(证明略)
上单调递增;(证明略)
所以,函数在定义域上不是单调递增或单调递减函数,从而该函数不是闭函数
(2) 先证 符合条件①:对于任意
符合条件①:对于任意

且 ,有
,有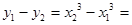

 ,
,  ,故
,故 是
是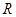 上的减函数.
上的减函数.
又因为 在
在 上的值域是
上的值域是 。
。
(3)易知 是
是 上的增函数,符合条件①;设函数符合条件②的区间为
上的增函数,符合条件①;设函数符合条件②的区间为 ,则
,则 ;故
;故 是
是 的两个不等根,即方程组为:
的两个不等根,即方程组为:
 有两个不等非负实根;
有两个不等非负实根;
设 为方程
为方程 的二根,则
的二根,则
解得:
 的取值范围
的取值范围 .
.
【解析】略

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本 万元(不含促销费用),每件产品的销售价格定为
万元(不含促销费用),每件产品的销售价格定为 元.
元. 万元表示为促销费用
万元表示为促销费用