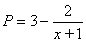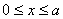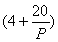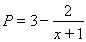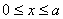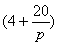题目内容
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录.为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足P=3-
(其中0≤x≤a,a为正常数).已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为(4+
)元/件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
| 2 |
| x+1 |
| 20 |
| P |
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
分析:(1)根据产品的利润=销售额-产品的成本建立函数关系;
(2)利用基本不等式可求出该函数的最值,注意等号成立的条件.
(2)利用基本不等式可求出该函数的最值,注意等号成立的条件.
解答:解:(1)由题意知,y=(4+
)P-x-(10+2P),
将P=3-
代入化简得:y=16-
-x (0≤x≤a).…(6分)
(2)y=17-(
+x+1)≤17-2
=13,
当且仅当
=x+1,即x=1时,上式取等号.…(9分)
当a≥1时,促销费用投入1万元时,厂家的利润最大;
当a<1时,y=17-(
+x+1)在[0,a]上单调递增,
所以x=a时,函数有最大值.即促销费用投入a万元时,厂家的利润最大.
综上,当a≥1时,促销费用投入1万元,厂家的利润最大;
当a<1时,促销费用投入a万元,厂家的利润最大.…(12分)
| 20 |
| P |
将P=3-
| 2 |
| x+1 |
| 4 |
| x+1 |
(2)y=17-(
| 4 |
| x+1 |
|
当且仅当
| 4 |
| x+1 |
当a≥1时,促销费用投入1万元时,厂家的利润最大;
当a<1时,y=17-(
| 4 |
| x+1 |
所以x=a时,函数有最大值.即促销费用投入a万元时,厂家的利润最大.
综上,当a≥1时,促销费用投入1万元,厂家的利润最大;
当a<1时,促销费用投入a万元,厂家的利润最大.…(12分)
点评:本题主要考查了函数模型的选择与应用,以及基本不等式在最值问题中的应用,同时考查了计算能力,属于中档题.

练习册系列答案
相关题目