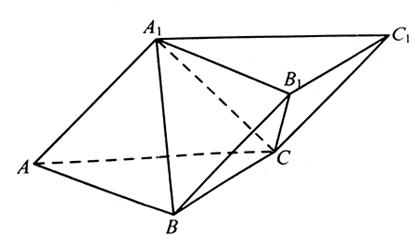
题目内容
在斜三棱柱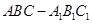 中,平面
中,平面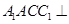 平面ABC,
平面ABC,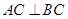 ,
,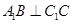 ,
,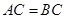 .
.
(1)求证: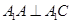 ;
;
(2)若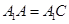 ,求二面角
,求二面角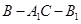 的余弦值.
的余弦值.
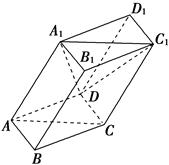
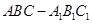 中,平面
中,平面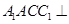 平面ABC,
平面ABC,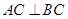 ,
,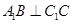 ,
,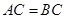 .
.(1)求证:
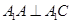 ;
;(2)若
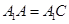 ,求二面角
,求二面角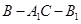 的余弦值.
的余弦值.
(1)证明过程详见解析;(2)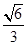 .
.
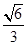 .
.试题分析:本题主要考查线线垂直、线面垂直、面面垂直、线线平行、二面角的余弦等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,利用面面垂直的性质得BC⊥平面A1ACC1,则利用线面垂直的性质得A1A⊥BC,由A1B⊥C1C,利用平行线A1A∥C1C,则A1A⊥A1B,利用线面垂直的判定得A1A⊥平面A1BC,则利用线面垂直的性质得A1A⊥A1C;第二问,建立空间直角坐标系,得到面上的点的坐标,计算出向量坐标,求出平面
 和平面
和平面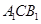 的法向量,利用夹角公式计算出二面角的余弦值.
的法向量,利用夹角公式计算出二面角的余弦值.(1)因为平面A1ACC1⊥平面ABC,AC⊥BC,所以BC⊥平面A1ACC1,
所以A1A⊥BC.
因为A1B⊥C1C,A1A∥C1C,所以A1A⊥A1B,
所以A1A⊥平面A1BC,所以A1A⊥A1C. 5分
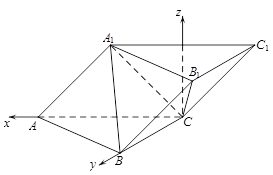
(2)建立如图所示的坐标系C-xyz.
设AC=BC=2,因为A1A=A1C,
则A(2,0,0),B(0,2,0),A1(1,0,1),C(0,0,0).
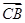 =(0,2,0),
=(0,2,0),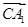 =(1,0,1),
=(1,0,1),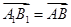 =(-2,2,0).
=(-2,2,0).设n1=(a,b,c)为面BA1C的一个法向量,则n1·
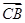 =n1·
=n1·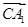 =0,
=0,则
 ,取n1=(1,0,-1).
,取n1=(1,0,-1).同理,面A1CB1的一个法向量为n2=(1,1,-1). 9分
所以cosán1,n2ñ=
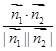 =
=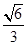 ,
,故二面角B-A1C-B1的余弦值为
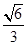 . 12分
. 12分
练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 中,
中, ,
, ,
,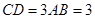 ,平面
,平面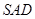 ⊥平面
⊥平面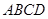 ,
,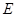 是线段
是线段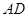 上一点,
上一点,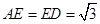 ,
,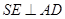 .
. ⊥平面
⊥平面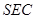 ;
; ,求直线
,求直线 与平面
与平面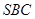 所成角的正弦值.
所成角的正弦值.
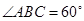 ,平面
,平面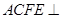 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a.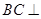 平面ACFE;
平面ACFE;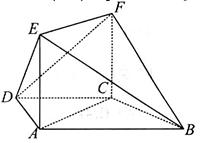
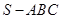 中,
中,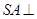 底面
底面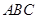 ,点
,点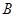 为以
为以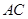 为直径的圆上任意一动点,且
为直径的圆上任意一动点,且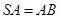 ,点
,点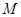 是
是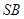 的中点,
的中点,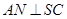 且交
且交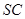 于点
于点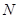 .
.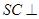 面
面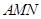 ;
;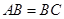 时,求二面角
时,求二面角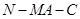 的余弦值.
的余弦值.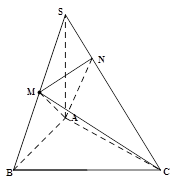
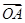 、
、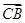 夹角θ的余弦值为( )
夹角θ的余弦值为( )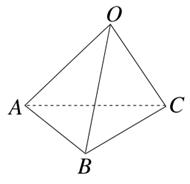
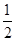
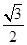
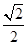
 中,
中,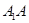
 底面
底面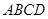 .四边形
.四边形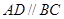 ,且
,且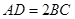 .过
.过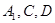 三点的平面记为
三点的平面记为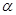 ,
,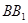 与
与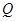 .
.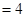 ,
,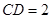 ,梯形
,梯形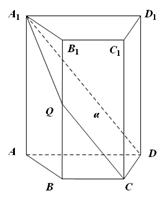
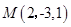 关于坐标原点对称的点是( )
关于坐标原点对称的点是( )