题目内容
设函数f(x)=loga(x+b)(a>0且a≠1),f(x)的反函数f-1(x)的图象与直线y=x的两个交点的横坐标分别为0、1.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)当点(x,y)是y=f(x)图象上的点时,点
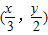 是函数y=g(x)上的点,求函数y=g(x)的解析式:
是函数y=g(x)上的点,求函数y=g(x)的解析式:(Ⅲ)在(Ⅱ)的条件下,当g
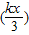 -f(x)≥0时,求x的取值范围(其中k是常数,且k≥
-f(x)≥0时,求x的取值范围(其中k是常数,且k≥ ).
).
【答案】分析:第一问可以利用互为反函数的两个函数图象关于y=x对称进行求解.
第二问可根据点(x,y)是y=f(x)图象上的点时,点 是函数y=g(x)上的点再结合第一问可列两个式y=f(x)=log2(x+1),
是函数y=g(x)上的点再结合第一问可列两个式y=f(x)=log2(x+1),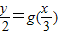 然后利用换元求解.
然后利用换元求解.
第三问在(1)(2)的条件下代入求解含参不等式,注意对根的大小进行分类讨论.
解答:解:(1)由题意知f-1(x)的图象与直线y=x的两个交点为(0,0),(1,1)
∴函数f(x)=loga(x+b)过(0,0),(1,1)两点
∴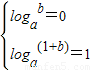 即b=1,a=2
即b=1,a=2
∴f(x)=log2(x+1)
(2)∵点(x,y)是y=f(x)图象上的点
∴y=f(x)=log2(x+1)
∵点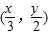 是函数y=g(x)上的点
是函数y=g(x)上的点
∴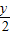 =g(
=g( )吗
)吗
∴ =g(
=g(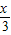 )
)
用3x代x:g(x)=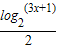
(3)∵g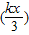 -f(x)≥0
-f(x)≥0
∴log2(kx+1)-2log2(x+1)≥0
∴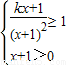 且kx+1>0且k≥
且kx+1>0且k≥
∴当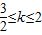 时 k-2≤x≤0
时 k-2≤x≤0
当 k>2时 0≤x≤k-2
点评:此题的综合性较强,层层递进,环环相扣.第二问考查了换元法求解析式,第三问考查了用分类讨论的思想接一元二次不等式.
第二问可根据点(x,y)是y=f(x)图象上的点时,点
 是函数y=g(x)上的点再结合第一问可列两个式y=f(x)=log2(x+1),
是函数y=g(x)上的点再结合第一问可列两个式y=f(x)=log2(x+1),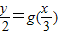 然后利用换元求解.
然后利用换元求解.第三问在(1)(2)的条件下代入求解含参不等式,注意对根的大小进行分类讨论.
解答:解:(1)由题意知f-1(x)的图象与直线y=x的两个交点为(0,0),(1,1)
∴函数f(x)=loga(x+b)过(0,0),(1,1)两点
∴
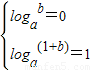 即b=1,a=2
即b=1,a=2∴f(x)=log2(x+1)
(2)∵点(x,y)是y=f(x)图象上的点
∴y=f(x)=log2(x+1)
∵点
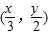 是函数y=g(x)上的点
是函数y=g(x)上的点∴
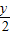 =g(
=g( )吗
)吗∴
 =g(
=g(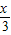 )
)用3x代x:g(x)=
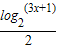
(3)∵g
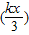 -f(x)≥0
-f(x)≥0∴log2(kx+1)-2log2(x+1)≥0
∴
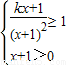 且kx+1>0且k≥
且kx+1>0且k≥
∴当
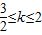 时 k-2≤x≤0
时 k-2≤x≤0当 k>2时 0≤x≤k-2
点评:此题的综合性较强,层层递进,环环相扣.第二问考查了换元法求解析式,第三问考查了用分类讨论的思想接一元二次不等式.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目