题目内容

如图，椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的四个顶点为A1，A2，B1，B2，两焦点为F1，F2，若以F1F2为直径的圆内切于菱形A1B1A2B2，切点分别为A，B，C，D，则菱形A1B1A2B2的面积S1与矩形ABCD的面积S2的比值
S1
S2
=（　　）
A．
5
+1
2
B．2
5
-2		C．
5
+2
2
D．
5
-1
2

菱形A1B1A2B2的面积S1=2ab，
设矩形ABCD，BC=2m，BA=2n，∴
m
n
=
a
b

∵m2+n2=c2，∴m=
ac
a2+b2
，n=
bc
a2+b2

∴面积S2=4mn=4•
abc2
a2+b2

∴
S1
S2
=
a2+b2
2c2

∵
c
a
=
b
a2+b2
，b2=a2-c2
∴a4-a2c2+c4=0
∴a4-3a2c2+c4=0
∴
a2
c2
=
3+
5
2
，
b2
c2
=
1+
5
2
，
∴
S1
S2
=
a2+b2
2c2
=
5
+2
4
．
故选C．
练习册系列答案
相关题目
【理科】抛物线顶点在原点，焦点是圆x2+y2-4x=0的圆心．
（1）求抛物线的方程；
（2）直线l的斜率为2，且过抛物线的焦点，与抛物线交于A、B两点，求弦AB的长；
（3）过点P（1，1）引抛物线的一条弦，使它被点P平分，求这条弦所在的直线方程．
抛物线y2=2px（p＞0），其准线方程为x=-1，过准线与x轴的交点M做直线l交抛物线于A、B两点．
（Ⅰ）若点A为MB中点，求直线l的方程；
（Ⅱ）设抛物线的焦点为F，当AF⊥BF时，求△ABF的面积．
过抛物线y2=4x的焦点作倾斜角为
π
3
的直线与抛物线交于点A、B，则|AB|=______．
已知点P在椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上，F1、F2分别为椭圆C的左、右焦点，满足|PF1|=6-|PF2|，且椭圆C的离心率为
5
3
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点Q（1，0）且不与x轴垂直的直线l与椭圆C相交于两个不同点M、N，在x轴上是否存在定点G，使得
GM
•
GN
为定值．若存在，求出所有满足这种条件的点G的坐标；若不存在，说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=它（a＞b＞0）的短轴长为2，离心率为
2
2
．
（它）求椭圆C的方程；
（2）若过点M（2，0）的引斜率为k的直线与椭圆C相交于两点G、H，设m为椭圆C上一点，且满足
OG
+
OH
=t
Om
（O为坐标原点），当|
mG
-
mH
|＜
2
5
3
时，求实数t的取值范围？
已知抛物线C：y2=2px（p＞0）的焦点为F，点K（-1，0）为直线l与抛物线C准线的交点．直线l与抛物线C相交于A，B两点，点A关于x轴的对称点为D．
（1）求抛物线C的方程；
（2）设
FA
•
FB
=
8
9
，求直线l的方程．
下列说法正确的是（　　） 
A．若两个角互补，则这两个角是邻补角；
B．若两个角相等，则这两个角是对顶角
C．若两个角是对顶角，则这两个角相等；
D．以上判断都不对
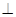已知AB为圆O的直径，AB=4，C为半圆上一点，过点C作圆O的切线CD，过点A作ADCD于D，交圆O于点E，DE=1，则BC的长为       。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网