题目内容
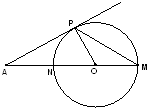（几何证明选讲选做题）如图，MN是圆O的直径，MN的延长线与圆O上过点P的切线PA相交于点A，若∠M=30°，切线AP长为2| 3 |
4
4
．分析：连接PN，由题设条件推导出△MPN中，ON=r，PM=2
，MN=2r，∠MPN=90°，由此能求出圆O的直径长．
| 3 |
解答：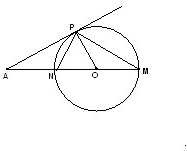
解：连接PN，
∵MN是圆O的直径，MN的延长线与圆O上过点P的切线PA相交于点A，
∠M=30°，切线AP长为2
，
∴∠MPN=∠APO=90°，
∠PNO=∠PON=60°，
∴∠A=30°，PM=2
，
∴△MPN中，ON=r，PM=2
，MN=2r，∠MPN=90°，
∴（4r）2=r2+（2
）2，
解得r=2．
∴圆O的直径长为4．
故答案为：4．
解：连接PN，∵MN是圆O的直径，MN的延长线与圆O上过点P的切线PA相交于点A，
∠M=30°，切线AP长为2
| 3 |
∴∠MPN=∠APO=90°，
∠PNO=∠PON=60°，
∴∠A=30°，PM=2
| 3 |
∴△MPN中，ON=r，PM=2
| 3 |
∴（4r）2=r2+（2
| 3 |
解得r=2．
∴圆O的直径长为4．
故答案为：4．
点评：本题考查与圆有关的比例线段的求法，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
名校课堂系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）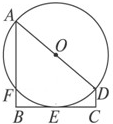
（几何证明选讲选做题）