Question

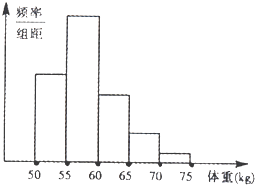
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:

(1)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率.

(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:

	箱产量<50kg	箱产量≥50kg
旧养殖法
新养殖法

(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).

P(K2≥k0)	0.050	0.010	0.001
k0	3.841	6.635	10.828

K2=

Answer 1

【答案】（1）；（2）有;(3).

【解析】试题分析：(1)根据小长方形面积等于对应区间概率分别计算旧养殖法的箱产量低于50kg 以及新养殖法的箱产量不低于50kg 的概率，最后根据概率乘法公式求事件A的概率，(2)根据数据对应填写即可，再根据卡方公式求K2，对照参考数据作把握率的判断，（3）先根据概率为0.5时对应区间，再设中位数根据概率为0.2列方程，解得中位数.

试题解析：

(1)记事件“旧养殖法的箱产量低于50kg”为事件B,记事件“新养殖法的箱产量不低于50kg”为事件C,

则P(A)=P(B)·P(C),

P(B)=5×(0.012+0.014+0.024+0.034+0.040)=0.62,

P(C)=5×(0.068+0.046+0.010+0.008)=0.66,

所以P(A)=0.4092.

(2)

	箱产量<50kg	箱产量≥50kg
旧养殖法	62	38
新养殖法	34	66

K2=≈15.705>6.635,

所以有99%的把握认为箱产量与养殖方法有关.

(3)方法一:因为新养殖法的箱产量分布图中,箱产量低于50kg的直方图面积为(0.004+0.020+0.044)×5=0.34<0.5,箱产量低于55kg的直方图面积为(0.004+0.020+0.044+0.068)×5=0.68>0.5.

故新养殖法箱产量的中位数的估计值为50+≈52.35.

方法二:由图可知,中位数位于50～55kg,首先计算小于50kg之前的频率为:(0.004+0.020+0.044)×5=0.340,设中位数为xkg,

则(x-50)×0.068=0.5-0.340=0.16,

解之得:x=52.35.

方法三:1÷5=0.2,0.1-(0.004+0.020+0.044)

=0.032,

0.032÷0.068=,×5≈2.35,

50+2.35=52.35,所以中位数为52.35.