题目内容
2.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a1004$\overrightarrow{OA}$+a1005$\overrightarrow{OC}$,且A,B,C三点共线(该直线不过原点O),则S2008等于1004.分析 根据条件,并由平面向量基本定理可得到a1004+a1005=1,而知道{an}为等差数列,根据前n项和公式即可求出S2008.
解答 解:A,B,C三点共线;
∴$\overrightarrow{AB}=k\overrightarrow{AC}$;
∴$\overrightarrow{OB}-\overrightarrow{OA}=k(\overrightarrow{OC}-\overrightarrow{OA})$;
∴$\overrightarrow{OB}=(1-k)\overrightarrow{OA}+k\overrightarrow{OC}$;
$\overrightarrow{OA},\overrightarrow{OC}$不共线,根据平面向量基本定理有:
$\left\{\begin{array}{l}{{a}_{1004}=1-k}\\{{a}_{1005}=k}\end{array}\right.$;
∴a1004+a1005=1;
∴S=1004(a1+a2008)=1004(a1004+a2005)=1004.
故答案为:1004.
点评 考查平面向量基本定理,共线向量基本定理,以及等差数列的通项公式及前n项和公式${S}_{n}=\frac{n({a}_{1}+{a}_{n})}{2}$.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
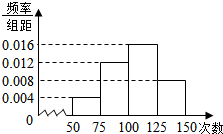 为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.
为了解初中生的身体素质,某地随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第2小组的频数是36,则n的值为120.