Question

13．若函数f（x）=k2^x-2^-x在（-∞，+∞）上是奇函数，则函数g（x）=log₂（x+k）的图象是（　　）

• A．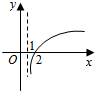
• B．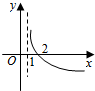
• C．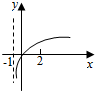
• D．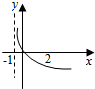

Answer 1

分析 由f（x）为奇函数，利用奇函数的性质确定出k的值，进而确定出g（x）解析式，得出其图象即可．

解答 解：∵函数f（x）=k2^x-2^-x在（-∞，+∞）上是奇函数，
∴f（-x）=-f（x），即k2^-x-2^x=-k2^x+2^-x，
解得：k=1，
则函数g（x）=log₂（x+k）=log₂（x+1）的图象是：
，
故选：C．

点评 此题考查了对数函数的图象与性质，以及奇函数的性质，熟练掌握对数函数的图象与性质是解本题的关键．