如图.正方形ABCD的边长为1.分别以定点A.B.C.D为圆心.以1为半径作弧.求图中阴影部分的面积．题目和参考答案——青夏教育精英家教网——

题目内容

5．如图，正方形ABCD的边长为1，分别以定点A、B、C、D为圆心，以1为半径作弧，求图中阴影部分的面积．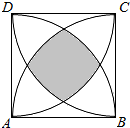

分析如图所示，设图中各部分面积分别为x，y，z，由题意可知图中三角形为等边三角形，利用扇形的面积，三角形面积公式，正方形面积公式可得关于x，y，z的方程组，解得z即为所求阴影部分的面积．

解答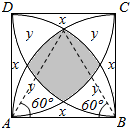解：如图所示，设图中各部分面积分别为x，y，z，
由题意得：4x+4y+z=1 ①，
2x+y=1-$\frac{α}{4}$ ②，
3x+2y=1-（2•$\frac{π}{6}$-$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×1）③，
③-②得，x+y=$\frac{3\sqrt{3}-π}{12}$ ④，
将④代入①得z=$\frac{3+π-3\sqrt{3}}{3}$．

点评本题主要考查了等边三角形和扇形的面积及不规则图形面积的计算，数形结合，利用规则图形的面积计算不规则图形的面积是解答此题的关键．

练习册系列答案

波波熊快乐暑假广西师范大学出版社系列答案

帮你学暑假作业科学普及出版社系列答案

通城学典暑期升级训练延边大学出版社系列答案

聪明屋寒暑假作业系列丛书暑假作业系列答案

暑假专题集训江苏人民出版社系列答案

优等生快乐暑假云南人民出版社系列答案

暑假学习生活译林出版社系列答案

成长记初中假期作业暑假云南教育出版社系列答案

暑假生活上海教育出版社系列答案

暑假天地重庆出版社系列答案

相关题目

15．若函数f（x）=4^x-2^x-a，x∈[-1，1]有零点，则实数a的取值范围是$[-\frac{1}{4}，2]$．

16．设a=0.7^0.7，b=0.7^1.6，c=1.6^0.7，则a，b，c的大小关系是（　　）

13．设$z=\frac{2}{1+i}+{（{1+i}）^2}$，则|$\overline{z}$|=（　　）

20．计算：
（1）lg5²+$\frac{2}{3}$lg8+lg5lg20+（lg2）²
（2）3${\;}^{\frac{1}{2}}$-27${\;}^{\frac{1}{6}}$+16${\;}^{\frac{3}{4}}$-2×（8${\;}^{-\frac{2}{3}}$）^-1+$\root{5}{2}$×（4${\;}^{-\frac{2}{5}}$）^-1．

10．设S_n为数列{a_n}的前n项和，若S_n=8a_n-1，则$\frac{{a}_{5}}{{a}_{3}}$=$\frac{64}{49}$．

17．若非零向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为钝角，|$\overrightarrow{b}$|=2，且当t=-$\frac{1}{2}$时，|$\overrightarrow{b}$-t$\overrightarrow{a}$|取最小值$\sqrt{3}$．向量$\overrightarrow{c}$满足（$\overrightarrow{c}-\overrightarrow{b}$）⊥（$\overrightarrow{c}-\overrightarrow{a}$），则当$\overrightarrow{c}•（\overrightarrow{a}+\overrightarrow{b}）$取最大值时，|$\overrightarrow{c}-\overrightarrow{b}$|等于（　　）

14．已知函数f（x）=$\left\{\begin{array}{l}{|lgx|，x＞0}\\{-{x}^{2}-2x，x≤0}\end{array}\right.$，
（1）分别求方程f（x）=1，方程f（x）=$\frac{1}{2}$的根的个数；
（2）试求关于x的函数y=2f²（x）-3f（x）+1的零点个数．

15．给出定义：连接平面点集内任意两点的线段中，线段的最大长度叫做该平面点集的长度，点集M由不等式组$\left\{\begin{array}{l}{2{x}^{2}-x-1≤0}\\{x-y+1≥0}\\{y≥0}\end{array}\right.$给出，点集M的长度是（　　）

$\frac{3\sqrt{2}}{2}$

$\frac{\sqrt{29}}{4}$