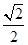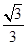题目内容
已知椭圆: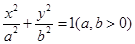 和圆
和圆 :
: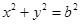 ,过椭圆上一点
,过椭圆上一点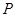 引圆
引圆 的两
的两
条切线,切点分别为 . 若椭圆上存在点
. 若椭圆上存在点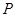 ,使得
,使得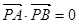 ,则椭圆离心率
,则椭圆离心率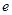 的取值范围
的取值范围
是( )
A. | B. | C.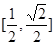 | D. |
D
解析试题分析:因为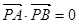 ,所以
,所以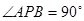 ,及圆的性质可得
,及圆的性质可得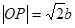 ,
,
所以 ,所以
,所以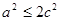 ,所以
,所以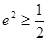 ,又因为
,又因为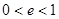 ,
,
所以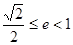 .
.
考点:椭圆的简单性质.
点评:本题考查直线与椭圆的位置关系,考查椭圆的几何性质,考查学生的计算能力,属于
基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
如图, 是平面
是平面 的斜线段,
的斜线段, 为斜足。若点
为斜足。若点 在平面
在平面 内运动,使得
内运动,使得 的面积为定值,则动点
的面积为定值,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 |
| C.一条直线 | D.两条平行直线 |
曲线 +
+ =1.(m<6) 与
=1.(m<6) 与 +
+ =1.(5<m<9)的( )
=1.(5<m<9)的( )
| A.准线相同 | B.离心率相同 | C.焦点相同 | D.焦距相同 |
若抛物线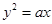 的焦点到准线的距离为4,则此抛物线的焦点坐标为
的焦点到准线的距离为4,则此抛物线的焦点坐标为
A.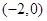 | B.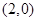 | C.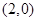 或 或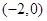 | D.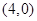 |
F1、F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=8,则点M的轨迹是( )
| A.线段 | B.直线 | C.椭圆 | D.圆 |
点 在直线
在直线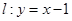 上,若存在过
上,若存在过 的直线交抛物线
的直线交抛物线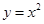 于
于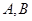 两点,且
两点,且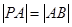 ,则称点
,则称点 为“
为“ 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )
A.直线 上的所有点都是“ 上的所有点都是“ 点” 点” | B.直线 上仅有有限个点是“ 上仅有有限个点是“ 点” 点” |
C.直线 上的所有点都不是“ 上的所有点都不是“ 点” 点” | D.直线 上有无穷多个点是“ 上有无穷多个点是“ 点” 点” |
抛物线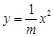 的焦点坐标为( )
的焦点坐标为( )
A.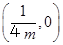 | B.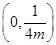 | C.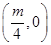 | D.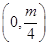 |
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )



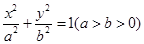 与双曲线
与双曲线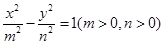 有相同的焦点
有相同的焦点 和
和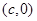 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为