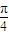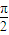Question

若函数y=sin⁴x+cos⁴x（x∈R），则函数的最小正周期为（　　）

• A、

  π

  4

• B、

  π

  2

• C、π
• D、2π

Answer 1

分析：直接根据同角三角函数之间的关系对函数进行化简，再结合正弦函数周期的求法即可得到结论．

解答：解：因为：y=sin⁴x+cos⁴x
=（sin²x+cos²x）²-2sin²x•cos²x
=1-

1

2

sin²2x=1-

1

2

•

1-cos4x

2

=1-

1-cos4x

4

=

3

4

+

cos4x

4

．
所以：所求周期T=

2π

4

=

π

2

，
故选B．

点评：本题主要考查三角函数中的恒等变换以及三角函数的周期的求法．函数y=Asin（ωx+φ）+b的周期公式为 T=

2π

|ω|

．