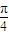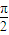题目内容
若函数y=sin4x+cos4x(x∈R),则函数的最小正周期为( )
A.
| B.
| C.π | D.2π |
因为:y=sin4x+cos4x
=(sin2x+cos2x)2-2sin2x•cos2x
=1-
sin22x=1-
•
=1-
=
+
.
所以:所求周期T=
=
,
故选B.
=(sin2x+cos2x)2-2sin2x•cos2x
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos4x |
| 2 |
=1-
| 1-cos4x |
| 4 |
=
| 3 |
| 4 |
| cos4x |
| 4 |
所以:所求周期T=
| 2π |
| 4 |
| π |
| 2 |
故选B.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
若函数y=sin4x+cos4x(x∈R),则函数的最小正周期为( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |