题目内容
 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE
(1)当平面A1DE⊥平面BCD时,求直线CD与平面A1CE所成角的正弦值;
(2)设M为线段A1C的中点,求证:在△ADE翻转过程中,BM的长度为定值.
解:(1)由矩形ABCD中,AB=2BC=4,E为边AB的中点,可得ED2=22+22=8=CE2,CD2=42=16,∴CE2+ED2=CD2,∴∠CED=90°,∴CE⊥ED.
又∵平面A1DE⊥平面BCD,∴CE⊥平面A1DE,∴CE⊥DA1.
又∵DA1⊥A1E,A1E∩EC=E,∴DA1⊥平面A1CE,∴∠A1CE即为直线CD与平面A1CE所成的角.
在Rt△A1CD中,sin∠A1CD=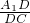 =
= .
.
(2)如图所示,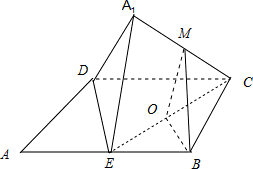
由(1)可知:CE⊥平面A1ED,∴∠A1ED为A1-EC-D的二面角的平面角,且为45°.
取CE的中点O,连接BO、MO,由三角形的中位线定理可知:MO∥AE,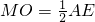 =1,∴MO⊥CE;
=1,∴MO⊥CE;
在等腰Rt△EBC中,CO=OE= ,则BO⊥CE.,∴∠MOB为二面角M-EC-B的平面角;
,则BO⊥CE.,∴∠MOB为二面角M-EC-B的平面角;
由图形可知:二面角A1-EC-D与二面角M-EC-B互补,因此二面角M-EC-B的平面角为135°.
又OB= ,在△MOB中,由余弦定理可得MB2=
,在△MOB中,由余弦定理可得MB2=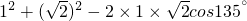 =5.
=5.
∴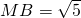 .
.
分析:(1)利用线面、面面垂直的判定和性质定理及线面角的定义即可求出;
(2)由二面角A1-EC-D为定值,且与二面角M-EC-B互补,及MO、BO为定值,即可得证.
点评:熟练掌握线面、面面垂直的判定和性质定理及线面角、二面角的定义及求法是解题的关键.
又∵平面A1DE⊥平面BCD,∴CE⊥平面A1DE,∴CE⊥DA1.
又∵DA1⊥A1E,A1E∩EC=E,∴DA1⊥平面A1CE,∴∠A1CE即为直线CD与平面A1CE所成的角.
在Rt△A1CD中,sin∠A1CD=
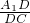 =
= .
.(2)如图所示,

由(1)可知:CE⊥平面A1ED,∴∠A1ED为A1-EC-D的二面角的平面角,且为45°.
取CE的中点O,连接BO、MO,由三角形的中位线定理可知:MO∥AE,
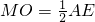 =1,∴MO⊥CE;
=1,∴MO⊥CE;在等腰Rt△EBC中,CO=OE=
 ,则BO⊥CE.,∴∠MOB为二面角M-EC-B的平面角;
,则BO⊥CE.,∴∠MOB为二面角M-EC-B的平面角;由图形可知:二面角A1-EC-D与二面角M-EC-B互补,因此二面角M-EC-B的平面角为135°.
又OB=
 ,在△MOB中,由余弦定理可得MB2=
,在△MOB中,由余弦定理可得MB2=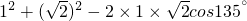 =5.
=5.∴
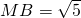 .
.分析:(1)利用线面、面面垂直的判定和性质定理及线面角的定义即可求出;
(2)由二面角A1-EC-D为定值,且与二面角M-EC-B互补,及MO、BO为定值,即可得证.
点评:熟练掌握线面、面面垂直的判定和性质定理及线面角、二面角的定义及求法是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是 如图,矩形ABCD中,
如图,矩形ABCD中, (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD