题目内容
(2009•朝阳区二模)已知集合A={(x,y)|y=|x-1|,x,y∈R},B={(x,y)|y=ax+2,x,y∈R},若集合A∩B有且只有一个元素,则实数a的取值范围是( )
分析:先画出两集合表示的曲线,集合A为定曲线,集合B为动曲线,即绕点(0,2)旋转的直线,故本题转化为两曲线有且只有一个交点时,动直线的斜率的取值范围问题,数形结合即可
解答:解:集合A中的点构成函数y=|x-1|的图象,集合B中的点是一条过定点(0,2),斜率为a的直线,如图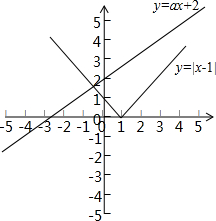
∵集合A∩B有且只有一个元素
∴函数y=|x-1|的图象与直线y=ax+2有且只有一个交点,数形结合可得a≥1或a≤-1
故选C
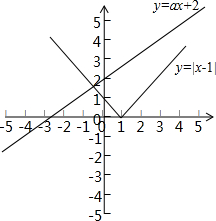
∵集合A∩B有且只有一个元素
∴函数y=|x-1|的图象与直线y=ax+2有且只有一个交点,数形结合可得a≥1或a≤-1
故选C
点评:本题考查了集合的表示方法及其几何意义,数形结合解决曲线交点个数问题,将集合问题转化为图形问题是解决本题的关键

练习册系列答案
相关题目