题目内容
已知关于x方程log2(x-1)+k-1=0在区间[2,5]上有实数根,那么k的取值范围是
[-1,1]
[-1,1]
.分析:方程即 log2(x-1)=1-k,由于当2≤x≤5时,0≤log2(x-1)≤2,由此可得 0≤1-k≤2,从而求得k的取值范围.
解答:解:关于x方程log2(x-1)+k-1=0,即 log2(x-1)=1-k.
当2≤x≤5时,0≤log2(x-1)≤2,
∴0≤1-k≤2,求得-1≤k≤1,
故答案为[-1,1].
当2≤x≤5时,0≤log2(x-1)≤2,
∴0≤1-k≤2,求得-1≤k≤1,
故答案为[-1,1].
点评:本题主要考查对数函数的单调性和特殊点,对数函数的定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
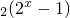 .若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
.若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.