题目内容
设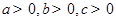 ,且
,且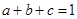 ,证明不等式:
,证明不等式: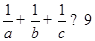
利用基本不等式证明即可
解析试题分析:因为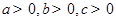 ,且
,且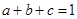 ,
,
所以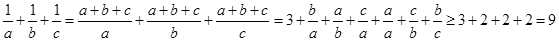 ,
,
当且仅当 时等号成立.
时等号成立.
考点:本小题主要考查不等式的证明和基本不等式的应用.
点评:解决本小题的关键是正确应用基本不等式,应用基本不等式的条件是“一正二定三相等”,三个条件缺一不可,还要注意“1”的整体代换.

练习册系列答案
相关题目
已知点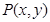 在不等式组
在不等式组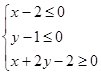 表示的平面区域上运动,则
表示的平面区域上运动,则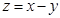 的取值范围是( )
的取值范围是( )
A.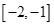 | B.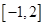 | C.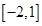 | D.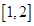 |
目标函数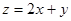 ,变量
,变量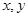 满足
满足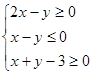 ,则有( )
,则有( )
A.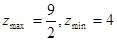 | B.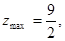  无最小值 无最小值 |
C. | D. 既无最大值,也无最小值 既无最大值,也无最小值 |

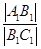 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;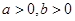 且
且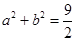 ,若
,若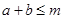 恒成立,
恒成立,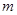 的最小值;
的最小值;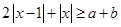 对任意的
对任意的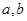 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.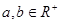 ,且
,且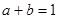 ,则
,则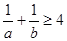 ;
;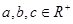 ,且
,且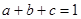 ,则
,则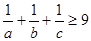 ;
;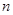 个正数
个正数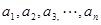 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。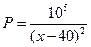 ,若要使每天获得的
,若要使每天获得的 利润最多,销售价格每件应定为多少元
利润最多,销售价格每件应定为多少元 ?
? (a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )