题目内容
17.在△OAB中$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别为$\overrightarrow{OA}$、$\overrightarrow{OB}$上的单位向量,∠AOB=120°,|OA|=3,且($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥$\overrightarrow{AB}$.(1)判断△OAB的形状;
(2)求S△OAB.
分析 (1)由题意$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$表示∠AOB的平分线,根据($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥$\overrightarrow{AB}$.可得Rt△OAE≌Rt△BOE,从而可得OA=OB.
(2)利用三角形面积公式即可得解.
解答 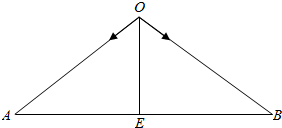 解:(1)∵$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别为$\overrightarrow{OA}$、$\overrightarrow{OB}$上的单位向量,
解:(1)∵$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别为$\overrightarrow{OA}$、$\overrightarrow{OB}$上的单位向量,
∴$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$表示∠AOB的平分线,
∵($\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥$\overrightarrow{AB}$.
∴Rt△OAE≌Rt△BOE,
∴OA=OB,
∴△BOA是等腰三角形.
(2)S△OAB=$\frac{1}{2}•$|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•sin∠AOB
=$\frac{1}{2}×3×3×sin120°$
=$\frac{9\sqrt{3}}{4}$.
点评 本题主要考查了三角形的形状判断,平面向量数量积的运算,角平分线的性质,三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
18.已知集合M={y|y=x2-1,x∈R},N={y|y=2-x2,x∈R},则M∩N等于( )
| A. | ∅ | B. | [-1,2] | C. | [-2,1] | D. | R |
2.某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是6元,销售单价与日均销售量的关系如下表:
请根据以上数据作出分析,这个经营部为获得最大利润应定价为12元.
| 销售单价/元 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 日均销售量/桶 | 440 | 400 | 360 | 320 | 280 | 240 | 200 |