题目内容
设函数f(x)的导数为f′(x),若f(x)=ax3-ax2+[(1)求f′(1);
(2)函数f(x)在R上不存在极值,求a的取值范围.
思路分析:求出f′(x),解关于f′(1)的方程,求得f′(1);要使f(x)在R上不存在极值,可先假定存在极值求出a的范围,然后取补集即为所求的范围.
解:(1)f′(x)=3ax2-2ax+![]() f′(1)-1,
f′(1)-1,
令x=1,得f′(1)=3a-2a+![]() f′(1)-1,
f′(1)-1,
所以f′(1)=2(a-1).
(2)当f(x)在R上存在极值时,令f′(x)=3ax2-2ax+a-2.
则Δ=4a2-12a(a-2)>0,解得0<a<3.
因此,要使函数f(x)在R上不存在极值,
只需a∈(-∞,0]∪[3,+∞).

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
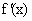 ,且
,且 ,则
,则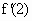 =________.
=________.