题目内容
设M是满足下列条件的函数f(x)构成的集合:“①方程f(x)-x=0有实数根;②函数f(x)的导数f′(x)满足0<f′(x)<1.”
(1)若函数f(x)为集合M中的任一元素,试证明方程f(x)-x=0只有一个实根;
(2)判断函数g(x)=![]() -
-![]() +3(x>1)是否是集合M中的元素,并说明理由;
+3(x>1)是否是集合M中的元素,并说明理由;
(3)“对于(2)中函数g(x)定义域内的任一区间[m,n],都存在x0∈[m,n],使得g(n)-g(m)=(n-m)g′(x0)”,请利用函数y=lnx的图像说明这一结论.
解析 (1)令h(x)=f(x)-x,则h′(x)=f′(x)-1<0,
即h(x)在区间(1,+∞)上单调递减.
所以,使h(x)=0,即f(x)-x=0成立的x至多有一解.
又由题设①知方程f(x)-x=0有实数根,
所以,方程f(x)-x=0只有一个实数根.
(2)由题意知,g′(x)=![]() -
-![]() ∈
∈![]() ⊂(0,1),满足条件.
⊂(0,1),满足条件.
令F(x)=g(x)-x=-![]() -
-![]() +3(x>1),
+3(x>1),
则F(e)=-![]() +
+![]() >0,F(e2)=-
>0,F(e2)=-![]() +2<0.
+2<0.
又F(x)在区间[e,e2]上连续,所以F(x)在[e,e2]上存在零点x0,即方程g(x)-x=0有实数根x0∈[e,e2],故g(x)满足条件①.
综上可知,g(x)∈M.
(3)由(1)知:g(n)-g(m)=![]() (n-m)-
(n-m)-![]() (lnn-lnm),
(lnn-lnm),
而(n-m)g′(x0)=(n-m)(![]() -
-![]() ),
),
所以原式等价于![]() =
=![]() .
.
该等式说明函数y=lnx(x>1)上任意两点A(m,lnm)和B(n,lnn)的连线段AB(如图所示),在曲线y=lnx(m≤x≤n)上都一定存在一点P(x0,lnx0),使得该点处的切线平行于AB,根据y=lnx(x>1)图像知该等式一定成立.


练习册系列答案
相关题目
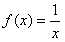 是否属于集合M?说明理由;
是否属于集合M?说明理由; 属于集合M,求实数a的取值范围。
属于集合M,求实数a的取值范围。  都在集合M中;
都在集合M中;