题目内容
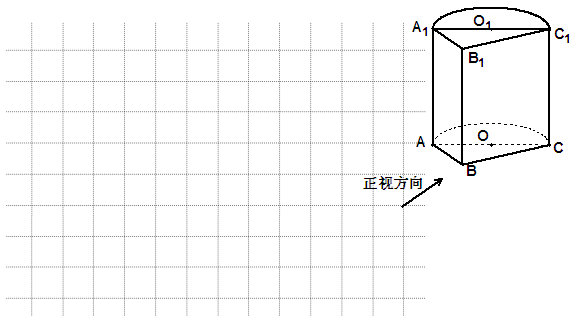
(本小题满分12分)如图,正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1.

(I)求证:A1C//平面AB1D;
(II)求二面角B—AB1—D的大小;
(III)求点C到平面AB1D的距离.

(I)求证:A1C//平面AB1D;
(II)求二面角B—AB1—D的大小;
(III)求点C到平面AB1D的距离.
(I)空间直角坐标系D—xyz,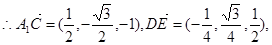
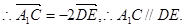
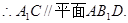 (II)
(II)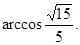 (III)
(III)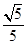
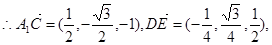
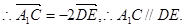
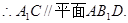 (II)
(II)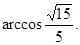 (III)
(III)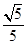
试题分析:建立空间直角坐标系D—xyz,如图,
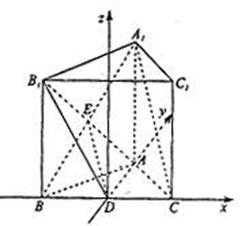
(1)证明:
连接A1B,设A1B∩AB1 = E,连接DE.
设A1A =" AB" = 1,
则
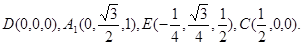
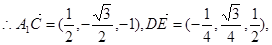
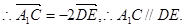 …………………………3分
…………………………3分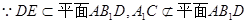 ,
,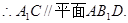 ……………………………………4分
……………………………………4分(2)解:
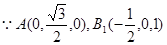 ,
, 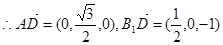 ,
,设
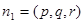 是平面AB1D的法向量,则
是平面AB1D的法向量,则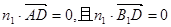 ,
,故
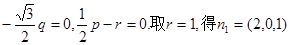 ;
;同理,可求得平面AB1B的法向量是
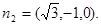 ……………………6分
……………………6分设二面角B—AB1—D的大小为θ,
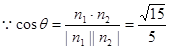 ,
,∴二面角B—AB1—D的大小为
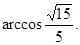 …………………………8分
…………………………8分(3)解由(II)得平面AB1D的法向量为
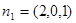 ,
,取其单位法向量
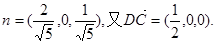
∴点C到平面AB1D的距离
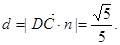
点评:本题第二问还可作出平面角求解,第三问利用等体积法亦可求解

练习册系列答案
相关题目
 是矩形,
是矩形, ,
,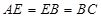 ,
,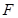 为
为 上的点,且
上的点,且 .
.
 ;
; .
.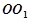 与三棱柱
与三棱柱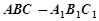 的组合体,其中,圆柱
的组合体,其中,圆柱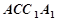 是边长为4的正方形,
是边长为4的正方形,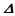
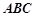 为等腰直角三角形,
为等腰直角三角形,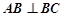 .
.
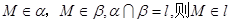 ;(4)空间中,相交于同一点的三条直线在同一平面内。
;(4)空间中,相交于同一点的三条直线在同一平面内。

 平面BCD;
平面BCD;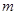 、
、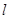 ,两个不同平面
,两个不同平面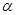 、
、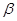 ,给出下列命题:
,给出下列命题: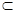
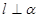 ,则
,则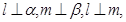 则
则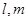 在平面
在平面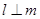 。
。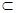 α,b
α,b