题目内容
△ABC的三边分别为a,b,c且满足b2=ac,2b=a+c,则此三角形形状是______.
由于△ABC的三边分别为a,b,c且满足 2b=a+c,∴4b2=(a+c)2 .
又∵b2=ac,∴(a-c)2 =0,∴a=c.
∴2b=a+c=2a,∴b=a,即a=b=c,故此三角形形状是 等边三角形,
故答案为 等边三角形.
又∵b2=ac,∴(a-c)2 =0,∴a=c.
∴2b=a+c=2a,∴b=a,即a=b=c,故此三角形形状是 等边三角形,
故答案为 等边三角形.

练习册系列答案
相关题目
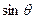 -
- ,
,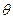 ∈(0,π),则tan
∈(0,π),则tan ABC中,cotA=
ABC中,cotA= ,则cosA="( " )
,则cosA="( " )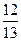



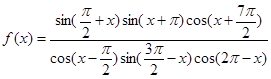 .
.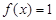 ,求
,求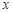 的取值构成的集合.
的取值构成的集合. ,求
,求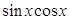 的值.
的值.