题目内容
已知f(x)=sinx+
cosx(x∈R).求:
(1)若x∈R,求f(x)的值域,并写出f(x)的单调递增区间;
(2)若x∈(-
,
),求f(x)的值域.
| 3 |
(1)若x∈R,求f(x)的值域,并写出f(x)的单调递增区间;
(2)若x∈(-
| π |
| 2 |
| π |
| 3 |
(1)由题意,f(x)=sinx+
cosx=2sin(x+
),
∴f(x)的值域为[-2,2],
令2kπ+
≤x+
≤2kπ-
,
解得2kπ-
≤x≤2kπ+
,
故函数的单调递增区间为[2kπ-
π,2kπ+
π],k∈Z;
(2)∵x∈(-
,
),
∴x+
∈(-
,
),
令t=x+
,则y=sint在(-
,
)上递增,在(
,
)上递减,
∴f(x)>sin(-
)=-
,fmax(x)=sin
=1,
∴-1<f(x)≤2,
故f(x)的值域为(-1,2].
| 3 |
| π |
| 3 |
∴f(x)的值域为[-2,2],
令2kπ+
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得2kπ-
| 5π |
| 6 |
| π |
| 6 |
故函数的单调递增区间为[2kπ-
| 5 |
| 6 |
| 1 |
| 6 |
(2)∵x∈(-
| π |
| 2 |
| π |
| 3 |
∴x+
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
令t=x+
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
∴f(x)>sin(-
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
∴-1<f(x)≤2,
故f(x)的值域为(-1,2].

练习册系列答案
相关题目

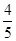 ,求S△AOB.
,求S△AOB.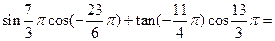 .
.