题目内容
(本题10分).在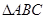 中,
中,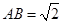 ,
,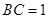 ,
,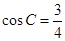 .
.
(1)求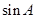 的值;(2)求
的值;(2)求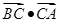 的值.
的值.
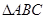 中,
中,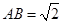 ,
,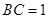 ,
,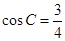 .
.(1)求
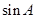 的值;(2)求
的值;(2)求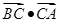 的值.
的值. (1)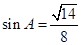 .(2)
.(2)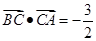 .
.
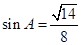 .(2)
.(2)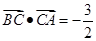 .
.(1)由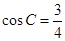 ,可得
,可得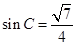 ,再利用正弦定理
,再利用正弦定理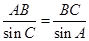 可求得
可求得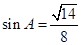 .
.
(2)先由余弦定理: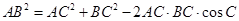 得:
得: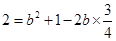 ,
,
进而得到b=2.再利用数理积的定义得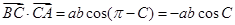 代入求值即可.
代入求值即可.
(1)在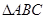 中,由
中,由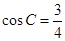 ,得
,得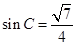 , 又由正弦定理:
, 又由正弦定理: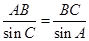 得:
得: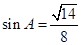 . ……………4分
. ……………4分
(2)由余弦定理: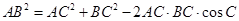 得:
得: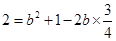 ,
,
即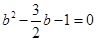 ,解得
,解得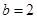 或
或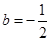 (舍去),所以
(舍去),所以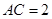 . ……8分
. ……8分
所以,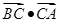
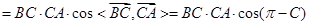

即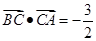 .
.
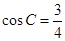 ,可得
,可得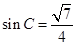 ,再利用正弦定理
,再利用正弦定理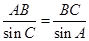 可求得
可求得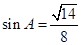 .
.(2)先由余弦定理:
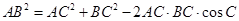 得:
得: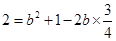 ,
,进而得到b=2.再利用数理积的定义得
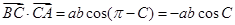 代入求值即可.
代入求值即可.(1)在
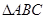 中,由
中,由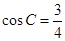 ,得
,得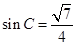 , 又由正弦定理:
, 又由正弦定理: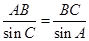 得:
得: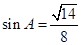 . ……………4分
. ……………4分(2)由余弦定理:
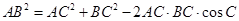 得:
得: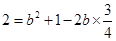 ,
,即
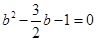 ,解得
,解得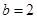 或
或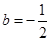 (舍去),所以
(舍去),所以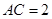 . ……8分
. ……8分所以,
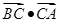
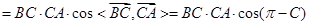

即
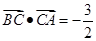 .
.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
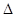 ABC中,BC=
ABC中,BC=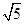 ,AC=3,sinC="2sinA"
,AC=3,sinC="2sinA"  的值.
的值.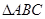 中,∠A、∠B的对边分别为a,b,且∠A=60°,
中,∠A、∠B的对边分别为a,b,且∠A=60°,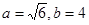 ,那么满足条件的
,那么满足条件的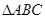 中,已知
中,已知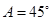 ,
,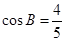 .
.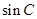 的值;
的值;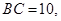 求
求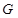 为△
为△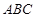 的重心,且
的重心,且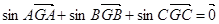 ,则
,则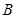 的大小为
的大小为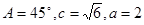 的△ABC的个数为m,则am的值为
的△ABC的个数为m,则am的值为  分别是角A,B,C的对边,
分别是角A,B,C的对边,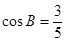 ,且
,且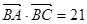 。
。 的值及△ABC的面积;
的值及△ABC的面积;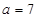 ,求角C的大小。
,求角C的大小。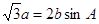 ,则
,则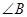 为
为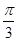
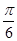
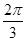
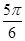
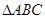 中,
中,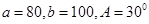 ,则
,则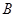 的解的个数是 ( )
的解的个数是 ( )