题目内容
若直线y=k(x-2)+1与曲线y=-
有两上不同的交点,则k的取值范围是( )
| 1-x2 |
A.[1,
| B.[1,
| C.(
| D.(0,
|
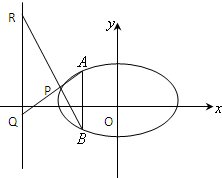
∵直线y=k(x-2)+1是过A(2,1)的直线,
曲线y=-
是圆心在原点,半径为1,y≤0的半圆,
∴作出如图图形:
当直线y=k(x-2)+1与半圆相切,C为切点时,圆心到直线l的距离d=r,
即
=1,
解得:k=
;
当直线y=k(x-2)+1过B(1,0)点时,直线l的斜率k=
=1,
∵直线y=k(x-2)+1与曲线y=-
有两上不同的交点,
∴k的取值范围是[1,
).
故选B.
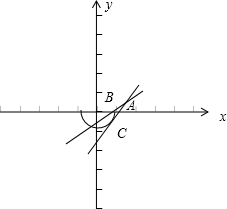
曲线y=-
| 1-x2 |
∴作出如图图形:
当直线y=k(x-2)+1与半圆相切,C为切点时,圆心到直线l的距离d=r,
即
| |k×0-0-2k+1| | ||
|
解得:k=
| 4 |
| 3 |
当直线y=k(x-2)+1过B(1,0)点时,直线l的斜率k=
| 1-0 |
| 2-1 |
∵直线y=k(x-2)+1与曲线y=-
| 1-x2 |
∴k的取值范围是[1,
| 4 |
| 3 |
故选B.


练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目