题目内容
【题目】如图,平面![]() 平面
平面![]() ,其中
,其中![]() 为矩形,
为矩形,![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)AB=![]() .
.
【解析】分析:(Ⅰ)由线面垂直的性质可得![]() 平面
平面![]() ,从而得
,从而得![]() ,结合
,结合![]() ,利用线面垂直的判定定理可得
,利用线面垂直的判定定理可得![]() 平面
平面![]() ;(Ⅱ)设
;(Ⅱ)设![]() ,以为
,以为![]() 原点,
原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴建立空间直角坐标系,平面ABF的法向量可取
轴建立空间直角坐标系,平面ABF的法向量可取![]() ,利用向量垂直数量积为零列方程组求得平面
,利用向量垂直数量积为零列方程组求得平面![]() 的法向量
的法向量![]() ),利用空间向量夹角余弦公式可得结果.
),利用空间向量夹角余弦公式可得结果.
详解:(Ⅰ)![]() 平面
平面![]() 平面
平面![]() ,且
,且![]() 为矩形,
为矩形,
![]()
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]()
![]() ,
,
又![]() 且
且![]()
![]() 平面
平面![]() .源:Z+xx+k.Com]
.源:Z+xx+k.Com]
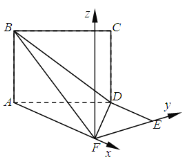
(Ⅱ)设AB=x.以F为原点,AF,FE所在的直线分别为x轴,y轴建立空间直角坐标系![]() .则F(0,0,0),A(-2,0,0),E(0,
.则F(0,0,0),A(-2,0,0),E(0,![]() ,0),D(-1,
,0),D(-1,![]() ,0),B(-2,0,x),所以
,0),B(-2,0,x),所以![]() =(1,-
=(1,-![]() ,0),
,0),![]() =(2,0,-x).
=(2,0,-x).
因为EF⊥平面ABF,所以平面ABF的法向量可取![]() =(0,1,0).
=(0,1,0).
设![]() =(x1,y1,z1)为平面BFD的法向量,则
=(x1,y1,z1)为平面BFD的法向量,则
所以,可取![]() =(
=(![]() ,1,
,1,![]() ).
).
因为cos<![]() ,
,![]() >=
>=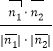 =
=![]() ,得x=
,得x=![]() ,所以AB=
,所以AB=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





