题目内容
给出下列结论:①y=1是幂函数;
②定义在R上的奇函数y=f(x)满足f(0)=0
③函数f(x)=lg(x+
)是奇函数
④当a<0时,(a2)
=a3
⑤函数y=1的零点有2个;
其中正确结论的序号是______(写出所有正确结论的编号).
②定义在R上的奇函数y=f(x)满足f(0)=0
③函数f(x)=lg(x+
| x2+1 |
④当a<0时,(a2)
| 3 |
| 2 |
⑤函数y=1的零点有2个;
其中正确结论的序号是______(写出所有正确结论的编号).
根据幂函数的定义可得y=1不是幂函数,故排除①.
由奇函数的定义可得定义在R上的奇函数y=f(x)满足f(0)=0,故②正确.
∵f(x)=lg(x+
),∴f(-x)=lg(-x+
)=lg(
)=-lg(x+
)=-f(x),
故函数f(x)=lg(x+
)是奇函数,故③正确.
当a<0时,(a2)
= [(-a)2]
=(-a)3=-a3,故④不正确.
由于函数y=1没有零点,故⑤不正确.
故答案为②③.
由奇函数的定义可得定义在R上的奇函数y=f(x)满足f(0)=0,故②正确.
∵f(x)=lg(x+
| x2+1 |
| x2+1 |
| 1 | ||
|
| x2+1 |
故函数f(x)=lg(x+
| x2+1 |
当a<0时,(a2)
| 3 |
| 2 |
| 3 |
| 2 |
由于函数y=1没有零点,故⑤不正确.
故答案为②③.

练习册系列答案
相关题目
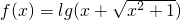 是奇函数
是奇函数 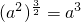
 是奇函数
是奇函数 