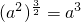题目内容
给出下列结论:①y=1是幂函数;②定义在R上的奇函数y=f(x)满足f(0)=0
③函数
 是奇函数
是奇函数 ④当a<0时,

⑤函数y=1的零点有2个;
其中正确结论的序号是 (写出所有正确结论的编号).
【答案】分析:根据幂函数的定义排除①.由奇函数的性质可得②正确.根据奇函数的定义可得③正确.根据a<0化简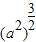 的结果为=-a3,故④不正确.根据函数y=1没有零点,得⑤不正确.由此得出结论.
的结果为=-a3,故④不正确.根据函数y=1没有零点,得⑤不正确.由此得出结论.
解答:解:根据幂函数的定义可得y=1不是幂函数,故排除①.
由奇函数的定义可得定义在R上的奇函数y=f(x)满足f(0)=0,故②正确.
∵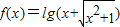 ,∴
,∴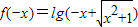 =
=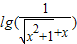 =-
=-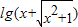 =-f(x),
=-f(x),
故函数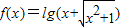 是奇函数,故③正确.
是奇函数,故③正确.
当a<0时,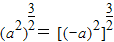 =(-a)3=-a3,故④不正确.
=(-a)3=-a3,故④不正确.
由于函数y=1没有零点,故⑤不正确.
故答案为②③.
点评:本题主要考查函数的奇偶性的判断、奇偶性性质,函数的零点及幂函数的定义,属于基础题.
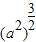 的结果为=-a3,故④不正确.根据函数y=1没有零点,得⑤不正确.由此得出结论.
的结果为=-a3,故④不正确.根据函数y=1没有零点,得⑤不正确.由此得出结论.解答:解:根据幂函数的定义可得y=1不是幂函数,故排除①.
由奇函数的定义可得定义在R上的奇函数y=f(x)满足f(0)=0,故②正确.
∵
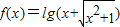 ,∴
,∴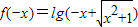 =
=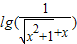 =-
=-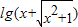 =-f(x),
=-f(x),故函数
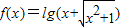 是奇函数,故③正确.
是奇函数,故③正确.当a<0时,
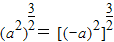 =(-a)3=-a3,故④不正确.
=(-a)3=-a3,故④不正确.由于函数y=1没有零点,故⑤不正确.
故答案为②③.
点评:本题主要考查函数的奇偶性的判断、奇偶性性质,函数的零点及幂函数的定义,属于基础题.

练习册系列答案
相关题目
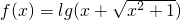 是奇函数
是奇函数