题目内容
已知曲线C1的方程是kx-y+4-2k=0(k∈R),曲线C2的方程是
+1-y=0,给出下列结论:
①曲线C1:恒过定点(2,4);
②曲线C2的图形是一个圆;
③k∈(
,+∞)时,C1与C2只有一个公共点;
④若k=0时,则C1与C2必无公共点.
其中正确结论的序号是
| 4-x2 |
①曲线C1:恒过定点(2,4);
②曲线C2的图形是一个圆;
③k∈(
| 3 |
| 4 |
④若k=0时,则C1与C2必无公共点.
其中正确结论的序号是
①③④
①③④
.分析:①利用直线的方程判断.②将曲线C2的方程进行化简判断.③利用直线与圆的位置关系判断.④利用直线与圆的位置关系判断.
解答:解:∵曲线C1的方程是kx-y+4-2k=0,
∴k(x-2)+4-y=0,表示过定点A(2,4)的直线,∴①正确.
∵C2的方程是
+1-y=0,
∴
=y-1,(y≥1),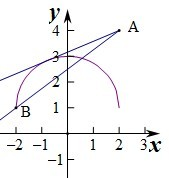
∴平方得x2+(y-1)2=4,表示以(0,1)为圆心,半径r=2的上半圆,∴②错误.
③当x=-2时,y=1,即B(-2,1),
此时过A,B直线的斜率k=
=
,由图象可知当k∈(
,+∞)时,C1与C2只有一个公共点,∴③正确.
④当k=0时,曲线C1的方程是y=4,
此时曲线C2的最大值为3,
∴则C1与C2无公共点,∴④正确.
故正确结论的序号是①③④.
故答案为:①③④.
∴k(x-2)+4-y=0,表示过定点A(2,4)的直线,∴①正确.
∵C2的方程是
| 4-x2 |
∴
| 4-x2 |

∴平方得x2+(y-1)2=4,表示以(0,1)为圆心,半径r=2的上半圆,∴②错误.
③当x=-2时,y=1,即B(-2,1),
此时过A,B直线的斜率k=
| 4-1 |
| 2-(-2) |
| 3 |
| 4 |
| 3 |
| 4 |
④当k=0时,曲线C1的方程是y=4,
此时曲线C2的最大值为3,
∴则C1与C2无公共点,∴④正确.
故正确结论的序号是①③④.
故答案为:①③④.
点评:本题主要考查直线与圆的方程以及直线与圆的位置关系的判断,利用数形结合是解决本题的关键.

练习册系列答案
相关题目