Question

已知数列的前n项和（n为正整数）。

（Ⅰ）令，求证数列是等差数列，并求数列的通项公式；

（Ⅱ）令，比较与的大小，并证明。（本小题满分14分）

Answer 1

（Ⅰ）.

（Ⅱ）当，当时

解析:

（I）在中，令n=1，可得，即

当时，，…… 2分

.

  .                   .   

 又数列是首项和公差均为1的等差数列. ……………………4分

 于是.……………………5分

(II)由（I）得，所以

由①-②得                  

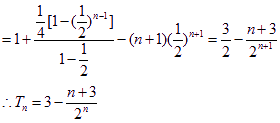
……………………8分

于是确定的大小关系等价于比较的大小

由                  

可猜想当证明如下：……………………10分

证法1：（1）当n=3时，由上验算显示成立。

（2）假设时

所以当时猜想也成立

综合（1）（2）可知 ，对一切的正整数，都有

证法2：当时

综上所述，当，当时