题目内容
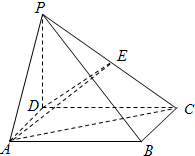 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为矩形,PD=DC=4,AD=2,E为PC的中点.
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为矩形,PD=DC=4,AD=2,E为PC的中点.(Ⅰ)求证:AD⊥PC;
(Ⅱ)求三棱锥A-PDE的体积;
(Ⅲ)AC边上是否存在一点M,使得PA∥平面EDM,若存在,求出AM的长;若不存在,请说明理由.
分析:(Ⅰ)要证AD⊥PC,先证AD⊥面PDC,就是从线面垂直进而推证线线垂直.
(Ⅱ)求三棱锥A-PDE的体积,先求底面PDE的面积,然后求解.
(Ⅲ)PA∥平面EDM,只要PA∥EM即可,找出再证明求解即可.
(Ⅱ)求三棱锥A-PDE的体积,先求底面PDE的面积,然后求解.
(Ⅲ)PA∥平面EDM,只要PA∥EM即可,找出再证明求解即可.
解答: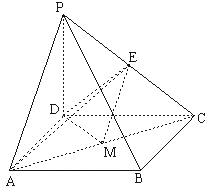 解:(Ⅰ)证明:因为PD⊥平面ABCD,
解:(Ⅰ)证明:因为PD⊥平面ABCD,
所以PD⊥AD.(2分)
又因为ABCD是矩形,
所以AD⊥CD.(3分)
因为PD∩CD=D,
所以AD⊥平面PCD.
又因为PC?平面PCD,
所以AD⊥PC.(5分)
(Ⅱ)解:因为AD⊥平面PCD,
所以AD是三棱锥A-PDE的高.
因为E为PC的中点,且PD=DC=4,
所以S△PDE=
S△PDC=
×(
×4×4)=4.(7分)
又AD=2,
所以VA-PDE=
AD•S△PDE=
×2×4=
.(9分)
(Ⅲ)解:取AC中点M,连接EM,DM,
因为E为PC的中点,M是AC的中点,
所以EM∥PA.
又因为EM?平面EDM,PA?平面EDM,
所以PA∥平面EDM.(12分)
所以AM=
AC=
.
即在AC边上存在一点M,使得PA∥平面EDM,AM的长为
.(14分)
 解:(Ⅰ)证明:因为PD⊥平面ABCD,
解:(Ⅰ)证明:因为PD⊥平面ABCD,所以PD⊥AD.(2分)
又因为ABCD是矩形,
所以AD⊥CD.(3分)
因为PD∩CD=D,
所以AD⊥平面PCD.
又因为PC?平面PCD,
所以AD⊥PC.(5分)
(Ⅱ)解:因为AD⊥平面PCD,
所以AD是三棱锥A-PDE的高.
因为E为PC的中点,且PD=DC=4,
所以S△PDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又AD=2,
所以VA-PDE=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
(Ⅲ)解:取AC中点M,连接EM,DM,
因为E为PC的中点,M是AC的中点,
所以EM∥PA.
又因为EM?平面EDM,PA?平面EDM,
所以PA∥平面EDM.(12分)
所以AM=
| 1 |
| 2 |
| 5 |
即在AC边上存在一点M,使得PA∥平面EDM,AM的长为
| 5 |
点评:本体是一道综合考查学生几何结构的题目,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=