题目内容
一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数m,n时,输出结果记为f(m,n),且计算装置运算原理如下:
①若Ⅰ、Ⅱ分别输入1,则f(1,1)=1;
②若Ⅰ输入固定的正整数,Ⅱ输入的正整数增大1,则输出结果比原来增大3;
③若Ⅱ输入1,Ⅰ输入正整数增大1,则输出结果为原来3倍.
试求:
(1)f(m,1)的表达式(m∈N);
(2)f(m,n)的表达式(m,n∈N);
(3)若Ⅰ、Ⅱ都输入正整数n,则输出结果f(n,n)能否为2013?若能,求出相应的n;若不能,则请说明理由.
①若Ⅰ、Ⅱ分别输入1,则f(1,1)=1;
②若Ⅰ输入固定的正整数,Ⅱ输入的正整数增大1,则输出结果比原来增大3;
③若Ⅱ输入1,Ⅰ输入正整数增大1,则输出结果为原来3倍.
试求:
(1)f(m,1)的表达式(m∈N);
(2)f(m,n)的表达式(m,n∈N);
(3)若Ⅰ、Ⅱ都输入正整数n,则输出结果f(n,n)能否为2013?若能,求出相应的n;若不能,则请说明理由.
考点:程序框图的三种基本逻辑结构的应用
专题:计算题,等差数列与等比数列
分析:(1)仔细审题,按照题设条件一步一步地进行转换,能够导出f(m,1)的表达式(m∈N).
(2)先由题设条件把f(m,n)转化为f(m,1)+3(n-1),从而得到其结果.
(3)由(7,7)=36+18=747<2013,f(8,8)=37+21=2208>2013,知f(n,n)输出结果不可能为2013.
(2)先由题设条件把f(m,n)转化为f(m,1)+3(n-1),从而得到其结果.
(3)由(7,7)=36+18=747<2013,f(8,8)=37+21=2208>2013,知f(n,n)输出结果不可能为2013.
解答:解:(1)f(m,1)=3f(m-1,1)=32f(m-2,1)=…=3m-1f(1,1)=3m-1,
(2)f(m,n)=f(m,n-1)+3=f(m,n-2)+3×2=…=f(m,1)+3(n-1)=3m-1+3(n-1),
(3)f(n,n)=3n-1+3(n-1),
∵f(7,7)=36+18=747<2013,f(8,8)=37+21=2208>2013
∴f(n,n)输出结果不可能为2013.
(2)f(m,n)=f(m,n-1)+3=f(m,n-2)+3×2=…=f(m,1)+3(n-1)=3m-1+3(n-1),
(3)f(n,n)=3n-1+3(n-1),
∵f(7,7)=36+18=747<2013,f(8,8)=37+21=2208>2013
∴f(n,n)输出结果不可能为2013.
点评:本题考查数列的递推式,题目比较新颖,解题的关键环节是认真审题,真正地理解题意.

练习册系列答案
相关题目
圆O1:x2+y2-2x=0和圆O2:x2+y2-4y=0的公切线条数( )
| A、1条 | B、2条 | C、3条 | D、4条 |
计算机执行如图程序段后,输出的结果是( )
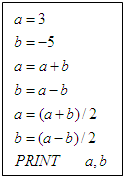
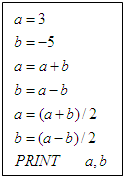
| A、0.5,-2.5 | B、3,-5 | C、0.5,-1.25 | D、-4.5,1.25 |
阅读如图所示程序框图,运行相应的程序,则输出的结果是( )
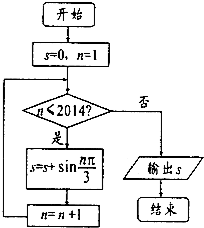

A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
某程序框图如图所示,该程序运行后输出的值是12,则判断框内可填入( )
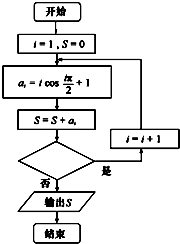

| A、i<5 | B、i<6 | C、i<7 | D、i<8 |
阅读如图所示的程序框图,运行相应的程序,若输入m=2014,n=6,则输出n的值为( )

| A、2014 | B、4 | C、3 | D、2 |
已知a是第三象限角,且tana=
,则sina等于( )
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
 上网获取信息已经成为人们日常生活的重要组成部分.因特网服务公司(Internet Service Provider)的任务就是负责将用户的计算机接入因特网,同时收取一定的费用.某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.公司A每小时收费1.5元;公司B的收费原则如图所示,即在用户上网的第1小时内收费1.7,第2小时内收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).假设一次上网时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?请写出其中的不等关系.
上网获取信息已经成为人们日常生活的重要组成部分.因特网服务公司(Internet Service Provider)的任务就是负责将用户的计算机接入因特网,同时收取一定的费用.某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.公司A每小时收费1.5元;公司B的收费原则如图所示,即在用户上网的第1小时内收费1.7,第2小时内收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).假设一次上网时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?请写出其中的不等关系.