题目内容
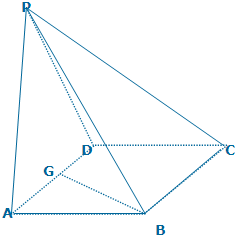 已知ABCD是边长为a,∠DAB=60°的菱形,点p为ABCD 所在平面外一点,面PAD为正三角形,其所在平面垂直于面ABCD
已知ABCD是边长为a,∠DAB=60°的菱形,点p为ABCD 所在平面外一点,面PAD为正三角形,其所在平面垂直于面ABCD(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC的中点,能否在PC上找到一F使平面DEF⊥平面ABCD.
分析:(1)连接BD,利用ABCD是边长为a,∠DAB=60°的菱形,G为AD的中点,推出BG⊥AD,然后证明BG⊥平面PAD;
(2)连接PG,利用PG⊥平面ABCD,BG是PB在平面ABCD内的射影,推出AD⊥PB;
(3)连接ED、GC交于点O,易得O为GC中点,通过作OF∥GP,交PC于点F,F为PC中点,说明FO⊥平面ABCD;即可证明结论.
(2)连接PG,利用PG⊥平面ABCD,BG是PB在平面ABCD内的射影,推出AD⊥PB;
(3)连接ED、GC交于点O,易得O为GC中点,通过作OF∥GP,交PC于点F,F为PC中点,说明FO⊥平面ABCD;即可证明结论.
解答: 证明:(1)连接BD,ABCD是边长为a,∠DAB=60°的菱形,
证明:(1)连接BD,ABCD是边长为a,∠DAB=60°的菱形,
G为AD的中点,∴BG⊥AD,平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD;
(2)连接PG,面PAD为正三角形,其所在平面垂直于面ABCD,
PG⊥平面ABCD,BG是PB在平面ABCD内的射影,
BG⊥AD,
∴AD⊥PB;
(3)连接ED、GC交于点O,易得O为GC中点,
在平面PGC内,作OF∥GP,交PC于点F,F为PC中点,
FO⊥平面ABCD;
∴平面DEF⊥平面ABCD.
 证明:(1)连接BD,ABCD是边长为a,∠DAB=60°的菱形,
证明:(1)连接BD,ABCD是边长为a,∠DAB=60°的菱形,G为AD的中点,∴BG⊥AD,平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD;
(2)连接PG,面PAD为正三角形,其所在平面垂直于面ABCD,
PG⊥平面ABCD,BG是PB在平面ABCD内的射影,
BG⊥AD,
∴AD⊥PB;
(3)连接ED、GC交于点O,易得O为GC中点,
在平面PGC内,作OF∥GP,交PC于点F,F为PC中点,
FO⊥平面ABCD;
∴平面DEF⊥平面ABCD.
点评:本题考查直线与平面的位置关系的证明,平面与平面的垂直,直线与直线的垂直,考查转化思想,空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
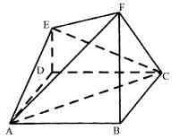 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2. 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.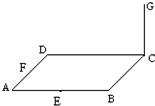 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离. 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.