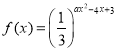Question

【题目】用两种颜色去染正九边形的顶点，每个顶点只染一种颜色，证明：在以这9点为顶点的所有三角形中，一定有两个顶点同色的全等三角形.

Answer 1

【答案】见解析

【解析】

至少有5个顶点涂以同色，不妨设为白色，这5个白点生成了个白色顶点的三角形.若绕正九边形的中心旋转，，则每次旋转九个顶点都与原有的顶点集合不变，但9次旋转白色顶点的共生成90个，而9个顶点共形成个三角形.

设原有顶点生成的三角形的集合为，则，其中5个顶点染自色，它们所生成的三角形，再经9次旋转之后，所生成的三角形的集合为，则.由于，且每个白色顶点三角形经9次旋转占有9个不同的位置，所以一定有两个白色顶点的三角形在旋转的过程中都与中的某一三角形重合.即存在，，有，，所以。