题目内容
11.已知函数f(x)=$\sqrt{3}$sinxcosx+tsin2x-$\frac{1}{2}$(t∈R)的图象过点($\frac{π}{12}$,0).(1)求t的值;
(2)△ABC中的角A、B、C的对边分别是a,b,c,若满足acosB+bcosA=2ccosB,求f(A)的取值范围.
分析 (1)利用三角恒等变换化简f(x)的解析式,再根据f(x)的图象经过点($\frac{π}{12}$,0)求得t的值,可得f(x)的解析式.
(2)由条件利用正弦定理求得B的值,可得A的范围,再利用正弦函数的定义域和值域求得f(A)的取值范围.
解答 解:(1)函数f(x)=$\sqrt{3}$sinxcosx+tsin2x-$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x+t•$\frac{1-cos2x}{2}$-$\frac{1}{2}$,
由f(x)的图象经过点($\frac{π}{12}$,0)可得$\frac{\sqrt{3}}{4}$+$\frac{t}{2}$-$\frac{\sqrt{3}}{4}$-$\frac{1}{2}$=0,求得t=1,
∴f(x)=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x=sin(2x-$\frac{π}{3}$).
(2)△ABC中,由acosB+bcosA=2ccosB,利用正弦定理可得sinAcosB+sinBcosA=2sinC•cosB,
化简可得sin(A+B)=2sinC•cosB,求得cosB=$\frac{1}{2}$,B=$\frac{π}{3}$.
故A∈(0,$\frac{2π}{3}$),∴2A-$\frac{π}{3}$∈(-$\frac{π}{3}$,π),f(A)=sin(2A-$\frac{π}{3}$)∈(-$\frac{\sqrt{3}}{2}$,1].
点评 本题主要考查正弦定理、三角恒等变换,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
12.如果A、B是独立事件,$\overline{A}$、$\overline{B}$分别是A、B的对立事件,那么以下等式不一定成立的是( )
| A. | P(AB)=P(A)•P(B) | B. | P($\overline{A}$•B)=P($\overline{A}$)•P(B) | C. | P(A+B)=P(A)+P(B) | D. | P($\overline{A}$•$\overline{B}$)=[1-P(A)][1-P(B)] |
19.已知集合A={1,3,9},B={1,9},则A∪B=( )
| A. | {1,3,9} | B. | {1,9} | C. | {3} | D. | {3,9} |
6.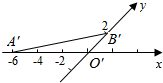 如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
 如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )| A. | 6 | B. | 3$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 12 |
16.已知结合A={x|y=$\sqrt{x+1}$},集合B={y|y=sinx},则下列结论正确的是( )
| A. | A∩B=∅ | B. | A∪B=B | C. | A∩B=A | D. | B?A |