题目内容

已知在空间直角坐标系中，有棱长为a的正方体ABCD-A1B1C1D1，点M是线段DC1上的动点，则点M到直线AD1距离的最小值为
 
．
考点：点、线、面间的距离计算
专题：计算题,向量法,空间位置关系与距离
分析：以A为坐标原点，AB，AD，AA1所在直线为x，y，z轴，建立空间直角坐标系，求出与两异面直线AD1和DC1均垂直的向量
n
，再由
AD
在
n
上的投影，即为点M到直线AD1距离的最小值．
解答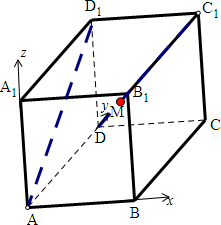： 解：如图以A为坐标原点，AB，AD，AA1所在直线为x，y，z轴，
建立空间直角坐标系，
则A（0，0，0），D（0，a，0），C1（a，a，a），
D1（0，a，a），
AD1
=（0，a，a），
DC1
=（a，0，a），
点M到直线AD1距离的最小值即为两异面直线AD1和DC1间的距离，
设它们的公垂线段所在的向量为
n
=（x，y，z），
则
n
⊥
AD1
，即有
n
•
AD1
=0，即为ay+az=0，
n
⊥
DC1
，即有
n
•
DC1
=0，即为ax+az=0，
可取
n
=（-1，-1，1），取
AD
=（0，a，0），
则两异面直线AD1和DC1间的距离为：
|
n
•
AD
|
|
n
|
=
a
3
=
3
3
a．
故答案为：
3
3
a．
点评：本题考查空间两异面直线的距离的求法，考查向量法求数量积和模，考查运算能力，属于中档题．
练习册系列答案
相关题目
函数y=1-2cos（
π
2
x）的周期为（　　）
A、2πB、1C、4D、2
若集合A={1，3，5}，集合B={1，2，3，4，5}，全集U={1，2，3，4，5，6，7，8}，求A∩B，A∪B，∁U（A∩B）．
已知sin(
π
2
+α)=
3
5
，则cosα的值是（　　）
A、-
3
5
B、±
3
5
C、
4
5
D、
3
5
已知3sinα+cosα=0，求下列各式的值．
（1）
3cosα+5sinα
sinα-cosα
；
（2）sin2α+2sinαcosα+cos2α．
y=x2-3x+2在∈[
1
2
，3]上的最小值与最大值分别为（　　）
A、
3
4
，2
B、-
1
4
，2
C、-
1
4
，
3
4
D、
3
4
，3
有下列命题：
（1）f（x）=sin（2x+
π
3
）的图象关于直线x=
π
12
对称；
（2）函数f（x）=4cos（2x+
π
3
）的图象关于点（-
5
12
π，0）对称；
（3）函数f（x）=tan（2x-
π
3
）的图象的所有对称中心为（
kπ
2
+
π
6
，0），k∈Z；
（4）如函数f（x）=4cos（2x+
π
3
），则由f （x1）=f （x2）=0可得x1-x2必是π的整数倍；
（5）函数f（x）=sin（ωx+φ）为奇函数的充要条件是φ=kπ+
π
2
，k∈Z．
其中正确的命题的序号是
 
．（注：把你认为正确的命题的序号都填上．）
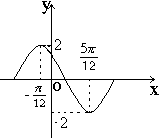函数y=Acos（ωx+φ）在一个周期内的图象如下，此函数的解析式为（　　）
A、y=2cos（2x+
π
6
）
B、y=2cos（2x-
π
6
）
C、y=2cos（
x
2
-
π
3
）
D、y=2cos（2x+
π
3
）
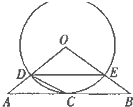如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC=CB．
（l）求证：直线AB是⊙O的切线；
（2）若AD=2，且tan∠ACD=
1
2
，求⊙O的半径r的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网