题目内容
【题目】已知函数![]()
(Ⅰ)求![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)说明函数![]() 的图像可由正弦曲线
的图像可由正弦曲线![]() 经过怎样的变化得到;
经过怎样的变化得到;
(Ⅲ)若![]() 是第二象限的角,求
是第二象限的角,求![]()
【答案】(Ⅰ)![]() ;(Ⅱ)如解析所示;(Ⅲ)
;(Ⅱ)如解析所示;(Ⅲ) ![]()
【解析】试题分析:(Ⅰ)直接根据周期公式即可求出最小正周期,通过正弦型复合函数的单调性求解增区间;(Ⅱ)可先平移后伸缩变换,也可先伸缩后平移变换得到;(Ⅲ)把![]() 代到(1)中的函数解析式,结合
代到(1)中的函数解析式,结合![]() 的范围求解
的范围求解![]() 的正余弦值,由二倍角可得答案.
的正余弦值,由二倍角可得答案.
试题解析:(Ⅰ)由![]() 可知,函数的最小正周期为
可知,函数的最小正周期为![]()
令![]() ,则
,则![]() 的增区间是
的增区间是![]() ,
,
由![]() ,解得
,解得![]()
所以函数![]() 的单调递增区间是
的单调递增区间是![]()
(Ⅱ)将![]() 和图像纵坐标不变, 横坐标为原来的
和图像纵坐标不变, 横坐标为原来的![]() 倍得到
倍得到![]() 的图像,将
的图像,将![]() 和图像向左平移
和图像向左平移![]() 得到
得到![]() 的图像,将
的图像,将![]() 的图像横坐标不变,纵坐标为原来的
的图像横坐标不变,纵坐标为原来的![]() 倍得到
倍得到![]() 的图像
的图像
或,将![]() 和图像向左平移
和图像向左平移![]() ,得到
,得到![]() 的图像,将
的图像,将![]() 纵坐标
纵坐标
不变,横坐标为原来的![]() 得到
得到![]() 的图像,将
的图像,将![]() 图像横坐标不变,纵坐标为原来的
图像横坐标不变,纵坐标为原来的![]() 倍得到
倍得到![]() 的图像.
的图像.
(Ⅲ)由![]() 知,所以
知,所以![]() ,即
,即![]() ,
,
又![]() 是第二象限的角,所以
是第二象限的角,所以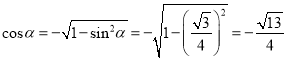 ,
,
所以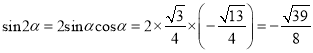

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目