题目内容
(本小题满分12分)
设递增等差数列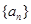 的前项和为
的前项和为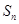 ,已知
,已知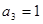 ,
,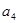 是
是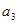 和
和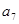 的等比中项。
的等比中项。
(1)求数列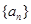 的通项公式;
的通项公式;
(2)求数列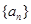 的前项和
的前项和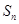
(1)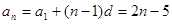 ;
;
(2) 。
。
解析

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
题目内容
(本小题满分12分)
设递增等差数列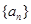 的前项和为
的前项和为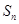 ,已知
,已知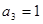 ,
,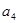 是
是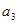 和
和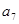 的等比中项。
的等比中项。
(1)求数列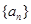 的通项公式;
的通项公式;
(2)求数列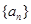 的前项和
的前项和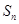
(1)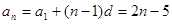 ;
;
(2) 。
。
解析

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案