题目内容
已知椭圆 :
: 与双曲线
与双曲线 有相同的焦点,且椭圆
有相同的焦点,且椭圆 的离心率
的离心率 ,又
,又 为椭圆的左右顶点,
为椭圆的左右顶点, 为椭圆上任一点(异于
为椭圆上任一点(异于 ).
).
(1)求椭圆的方程;
(2)若直线 交直线
交直线 于点
于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 轴于点
轴于点 ,求
,求 的坐标;
的坐标;
(3)求点 在直线
在直线 上射影
上射影 的轨迹方程.
的轨迹方程.

【答案】
(1)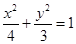 ;(2);
;(2);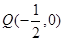 (3)
(3)
【解析】(1) 由题意知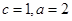 ,易知椭圆方程为
,易知椭圆方程为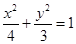
(2)本小题的求解要注意利用平面几何的性质得到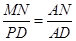 ,另外要注意应用
,另外要注意应用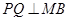 ,点M在椭圆上等几何要素建立方程求解即可.
,点M在椭圆上等几何要素建立方程求解即可.
(3) 点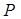 在直线
在直线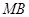 上射影即PQ与MB的交点H,由
上射影即PQ与MB的交点H,由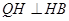 得
得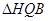 为直角三角形,设E为
为直角三角形,设E为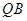 中点,则
中点,则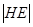 =
=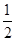
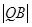 =
=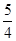 ,
,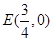 ,因此H点的轨迹是以E为圆心,半径为
,因此H点的轨迹是以E为圆心,半径为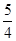 的圆去掉与x轴的交点.
的圆去掉与x轴的交点.
解:(Ⅰ)由题意知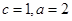 ,故椭圆方程为
,故椭圆方程为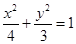 3分
3分
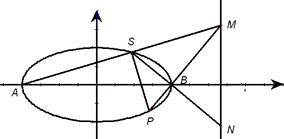
(Ⅱ)设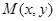 ,
,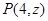 则由图知
则由图知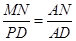 ,得
,得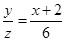 ,故
,故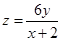 .
.
设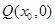 ,由
,由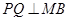 得:
得: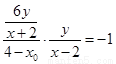 ,
, 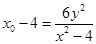 .
.
又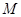 在椭圆上,故
在椭圆上,故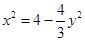 ,化简得
,化简得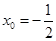 ,即
,即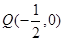 8分
8分
(Ⅲ)点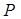 在直线
在直线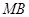 上射影即PQ与MB的交点H,由
上射影即PQ与MB的交点H,由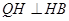 得
得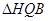 为直角三角形,设E为
为直角三角形,设E为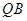 中点,则
中点,则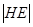 =
=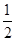
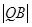 =
=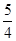 ,
,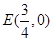 ,因此H点的轨迹方程为
,因此H点的轨迹方程为
 13分
13分

练习册系列答案
相关题目
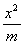 +
+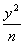 =1(
=1(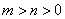 )与双曲线
)与双曲线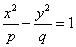 (
(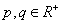 )有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。
)有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。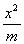 +
+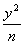 =1(
=1(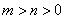 )与双曲线
)与双曲线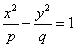 (
(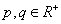 )有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。
)有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。