题目内容
已知椭圆![]() :
:![]() 与双曲线
与双曲线![]() 有公共焦点,且离心率为
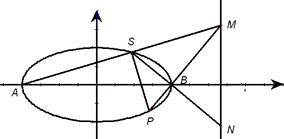
有公共焦点,且离心率为![]() .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:![]() 分别交于M,N两点.
分别交于M,N两点.
(1)求椭圆C的方程;
(2)延长MB交椭圆C于点P,若PS⊥AM,试证明MS2=MB·MP.
(3)当线段MN的长度最小时,在椭圆C上是否存在点T,使得△TSB的面积为![]() ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.
答案:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
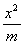 +
+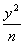 =1(
=1(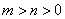 )与双曲线
)与双曲线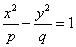 (
(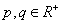 )有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。
)有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。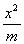 +
+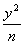 =1(
=1(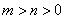 )与双曲线
)与双曲线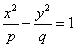 (
(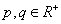 )有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。
)有共同的焦点F1、F2 ,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。