题目内容
已知椭圆C1与双曲线C2有相同的焦点F1、F2，点P是C1与C2的一个公共点，△PF1F2是一个以PF1为底的等腰三角形，，|PF1|=4，C1的离心率为
，则C2的离心率为
| 3 | 7 |
3
3
．分析：利用离心率的定义，及C1的离心率e1=
，|PF1|=4，|F1F2|=|PF2|，可求得|PF2|=3，再利用双曲线的离心率e2=
，可得结论．
| 3 |
| 7 |
| |F1F2| |
| |PF1|-|PF2| |
解答：解：由题意知C1的离心率e1=
=
=
=
，
又|PF1|=4，|F1F2|=|PF2|，
∴|PF2|=3
∴双曲线的离心率e2=
=3
故答案为：3
| c1 |
| a1 |
| 2c1 |
| 2a1 |
| |F1F2| |
| |PF1|+|PF2| |
| 3 |
| 7 |
又|PF1|=4，|F1F2|=|PF2|，
∴|PF2|=3
∴双曲线的离心率e2=
| |F1F2| |
| |PF1|-|PF2| |
故答案为：3
点评：本题考查椭圆与双曲线的几何性质，解题的关键是正确运用离心率的定义，属于中档题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
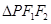是一个以PF1为底的等腰三角形，
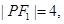C1的离心率为
则C2的离心率