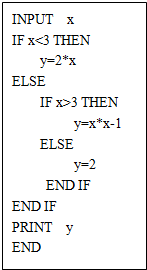题目内容
14．已知函数f（x）=x2+lnx-ax在（0，1）上是增函数，则实数a的取值范围是（-∞，$2\sqrt{2}$]．分析 根据函数f（x）是增函数，等价为f′（x）≥0在（0，1）上恒成立，即可得到结论．
解答 解：函数的定义域为（0，+∞），要使f（x）=lnx+x2-ax在定义域内是增函数，
则等价为f′（x）≥0在（0，1）上恒成立，
∵f（x）=lnx+x2-ax，
∴f′（x）=$\frac{1}{x}$+2x-a≥0，
即a≤$\frac{1}{x}$+2x在x∈（0，1）上恒成立，
当x＞0时，y=$\frac{1}{x}$+2x≥2$\sqrt{2x•\frac{1}{x}}$=2$\sqrt{2}$，当且仅当x=$\frac{\sqrt{2}}{2}$时取等号．
则a≤2$\sqrt{2}$，
故答案为：（-∞，$2\sqrt{2}$]．
点评 本题主要考查函数单调性的应用和判断，根据函数导数和单调性之间的关系转化为函数恒成立即可得到结论．
练习册系列答案
相关题目
9．命题p：函数$y=x+\frac{2}{x}$在[1，4]上的值域为$[{3，\frac{9}{2}}]$；命题$q：log_{\frac{1}{2}}^{（a+1）}＞log_{\frac{1}{2}}^a（a＞0）$．下列命题中，真命题的是（ ）
| A． | p∧q | B． | ￢p∨q | C． | p∧￢q | D． | p∨q |
6．
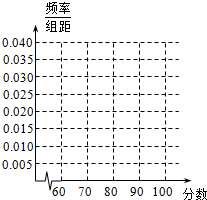为纪念中国抗日战争胜利70周年，某中学高三年级举办了“铭记历史，开创未来”的抗战历史知识竞赛活动，共有1000名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，请你根据频率分布表，解答下列问题：
（1）写出频率分布表中①、②所代表的数据；
（2）在所给坐标系中画出样本的频率分布直方图；
（3）为鼓励更多的学生了解“抗战历史”知识，对成绩不低于90分的学生给予奖励，请估计在参加竞赛的1000名学生中大概有多少名学生获奖．
为纪念中国抗日战争胜利70周年，某中学高三年级举办了“铭记历史，开创未来”的抗战历史知识竞赛活动，共有1000名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，请你根据频率分布表，解答下列问题：| 序号 | 分组 | 频数 | 频率 |
| 1 | [60，70） | ① | 0.15 |
| 2 | [70，80） | 20 | 0.2 |
| 3 | [80，90） | 35 | 0.35 |
| 4 | [90，100） | 30 | ② |
| 合计 | 100 | 1 | |
（2）在所给坐标系中画出样本的频率分布直方图；
（3）为鼓励更多的学生了解“抗战历史”知识，对成绩不低于90分的学生给予奖励，请估计在参加竞赛的1000名学生中大概有多少名学生获奖．