题目内容
定义域为R的函数f(x)满足:对于任意的实数x,y都有f(x+y)=f(x)+f(y)成立,且当x>0时f(x)<0恒成立.
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)证明f(x)为减函数;若函数f(x)在[-3,3)上总有f(x)≤6成立,试确定f(1)应满足的条件;
(3)解关于x的不等式![]() f(ax2)-f(x)>
f(ax2)-f(x)>![]() f(a2x)-f(a),(n是一个给定的自然数,a<0.)
f(a2x)-f(a),(n是一个给定的自然数,a<0.)
解析:
|
解:(1)由已知对于任意x∈R,y∈R,f(x+y)=f(x)+f(y)恒成立 令x=y=0,得f(0+0)=f(0)+f(0),∴f(0)=0 令x=-y,得f(x-x)=f(x)+f(-x)=0 ∴对于任意x,都有f(-x)=-f(x). ∴f(x)是奇函数. (2)设任意x1,x2∈R且x1<x2,则x2-x1>0,由已知f(x2-x1)<0 ① 又f(x2-x1)=f(x2)+f(-x1)=f(x2)-f(-x1) ② 由①,②得f(x1)>f(x2),根据函数单调性的定义知f(x)在(-∞,+∞)上是减函数. ∴f(x)在[-3,3]上的最大值为f(-3).要使f(x)≤6恒成立,当且仅当f(-3)≤6, 又∵f(-3)=-f(3)=-f(2+1)=-[f(2)+f(1)]=-[f(1)+f(1)+f(1)]=-3f(1), ∴f(1)≥-2. (3) 由已知得:f[n(x-a)]=nf(x-a) ∴f(ax2-a2x)>f[n(x-a)] ∵f(x)在(-∞,+∞)上是减函数 ∴ax2-a2x<n(x-a). 即(x-a)(ax-n)<0, ∵a<0, ∴(x-a)(x- 讨论: ①当a< ②当a= ③当 原不等式的解集为{x|x>a或x< |

 名校课堂系列答案
名校课堂系列答案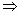 f(ax2)-f(a2x)>n[f(x)-f(a)]
f(ax2)-f(a2x)>n[f(x)-f(a)] )>0,
)>0,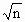 时,原不等式解集为{x|x>
时,原不等式解集为{x|x>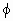
 选考题
选考题 定义域为R,求实数m的取值范围.
定义域为R,求实数m的取值范围. 上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与半圆C上的弧AP的长度均为
上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与半圆C上的弧AP的长度均为