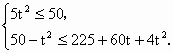Question

解答题

某地为促进淡水养殖业的发展，将价格控制在适当的范围内，决定对淡水鱼养殖提供政府补贴．设谈水鱼的市场价格为x元/千克，政府补贴为t元/千克，根据市场调查，当8≤x≤14时，淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系：P＝1000(x＋t－8)(x≥8，t≥0)，Q＝500(8≤x≤14)．当P＝Q时的市场价格称为市场平衡价格．

(1)将市场平衡价格表示为政府补贴的函数，并求出函数的定义域；

(2)为使市场平衡价格不高于每千克10元，政府补贴至少为每千克多少元？

Answer 1

答案：
解析：

解：(1)依题意P＝Q，从而1000(x＋t－8)＝500． 　　∴2[(x－8)＋t]＝． 　　平方得5(x－8)2＋8t(x－8)＋4t2－40＝0． 　　[(x－8)＋t]2＝8－t2． 　　当8－t2≥0时，x＝8－t±． 　　∵x≥8，∴x＝8－y＋． 　　由t≥0，8－t2≥0，0≤x－8≤6．可得0≤t≤5　　① 　　且0≤－t＋≤6 　　2t≤≤15＋2t4t2≤50－t2≤(15＋2t)2 　　∴0≤t≤　　② 　　求①、②的交集得0≤t≤． 　　故所求函数的定义域为[0，]． 　　(2)为使x≤10，应有8－t＋≤10． 　　∴5＋2t≥． 　　两边平方，化简得t2＋4t－5≥0． 　　从而得t≥1或t≤－5． 　　由于t≥0，∴t≥1． 　　∴政府补贴至少每千克1元．